Capítulo 9 Datos estructurados
Scripts usados:
Ya sabemos un poco la gramática y ortografía de nuestro lenguaje, y algunas de las funcionalidades básicas de nuestro «Word». Vamos a introducir cómo escribir la mejor trama para la novela: hablemos por fin de datos (introducción muy reducida).
9.1 Matrices
Hasta ahora, si quisiéramos trabajar con los datos de una persona y lo imaginamos en un Excel, hemos aprendido algunos tipos básicos que pueden tomar las celdas, y hemos aprendido a formar columnas (vectores, colecciones de elementos del mismo tipo).
Pero hasta ahora cada columna la hemos tratado por separado: una colección de números, otra de caracteres, fechas, etc. Pero de momento solo hemos visto solo datos en una dimensión: una sola variable de \(n\) elementos.
# Ejemplos de variables unidimensionales (vectores)
c(1, 4, NA, -2, 0)## [1] 1 4 NA -2 0
c("a", NA, "b", "c")## [1] "a" NA "b" "c"
c(TRUE, TRUE, FALSE, TRUE)## [1] TRUE TRUE FALSE TRUE## [1] "2022-09-14" "2022-09-15" "2022-09-16"Pero cuando analizamos datos solemos tener varias variables distintas de cada individuo, por ejemplo, la estatura y el peso de una persona. Necesitamos una «tabla», una manera de unir distintas variables numéricas, todas de IGUAL longitud. Y ese conjunto de variables (del mismo tipo e igual longitud), dispuestas en columnas, es lo que conocemos como matrices: una «tabla» de valores del mismo tipo, con filas y columnas.
Vamos a empezar definiendo una matriz sencilla: imagina que tenemos las estaturas y pesos de 5 personas.
¿Cómo juntar las dos variables creando nuestro primer conjunto de datos? Vamos a crear una matriz, un conjunto de números organizado en 2 columnas (una por variable) y 5 filas o registros (una por persona). Para ello usaremos la función cbind(), que nos concatena vectores de igual longitud en columnas.
datos_matriz <- cbind(estaturas, pesos) # Construimos la matriz por columnas
datos_matriz # nuestra primera matriz## estaturas pesos
## [1,] 150 60
## [2,] 160 70
## [3,] 170 80
## [4,] 180 90
## [5,] 190 100Nuestro primer conjunto de datos :) Podemos visualizar la matriz en un formato «excelizado» con la función View()
View(datos_matriz)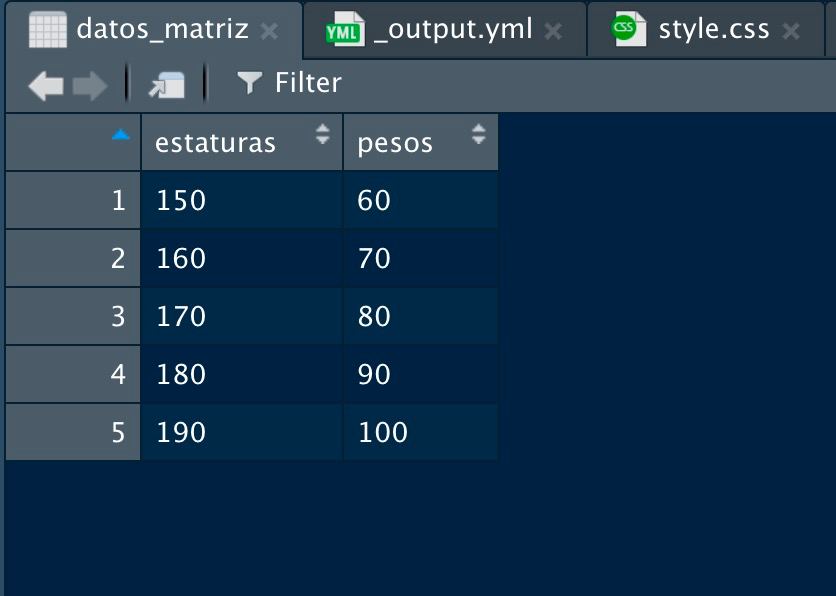
Imagen/gráfica 9.1: Nuestra primera matriz de datos
También podemos construir la matriz por filas con el comando rbind(), que nos permite añadir filas a una matriz o construirla desde cero (aunque lo habitual y recomendable es tener cada variable en una columna y cada individuo en una fila).
rbind(estaturas, pesos) # Construimos la matriz por filas## [,1] [,2] [,3] [,4] [,5]
## estaturas 150 160 170 180 190
## pesos 60 70 80 90 100Para practicar vamos a definir otro ejemplo, con las edades, teléfonos y códigos postales de una serie de individuos (fíjate que hay adrede datos ausentes, ya que a veces no tendremos datos de algunas personas de algunas variables).
edades <- c(14, 24, 56, 31, 20, 87, 73) # vector numérico de longitud 7
tlf <- c(NA, 683839390, 621539732, 618211286, NA, 914727164, NA)
cp <- c(33007, 28019, 37005, 18003, 33091, 25073, 17140)
# Construimos la matriz por columnas
datos_matriz <- cbind(edades, tlf, cp)
datos_matriz## edades tlf cp
## [1,] 14 NA 33007
## [2,] 24 683839390 28019
## [3,] 56 621539732 37005
## [4,] 31 618211286 18003
## [5,] 20 NA 33091
## [6,] 87 914727164 25073
## [7,] 73 NA 17140De nuevo tenemos una tabla de números: una columna por variable y una fila por registro. Los comandos cbind() y rbind() no solo nos permiten crear matrices desde cero sino también añadir filas o columnas a matrices existentes.
## edades tlf cp
## [1,] 14 NA 33007
## [2,] 24 683839390 28019
## [3,] 56 621539732 37005
## [4,] 31 618211286 18003
## [5,] 20 NA 33091
## [6,] 87 914727164 25073
## [7,] 73 NA 17140
## [8,] 27 620125780 28051## edades tlf cp estaturas
## [1,] 14 NA 33007 160
## [2,] 24 683839390 28019 155
## [3,] 56 621539732 37005 170
## [4,] 31 618211286 18003 181
## [5,] 20 NA 33091 174
## [6,] 87 914727164 25073 NA
## [7,] 73 NA 17140 165Como ves, ahora nuestros datos están tabulados, tienen dos dimensiones. ¿Cómo saber las dimensiones que tiene una matriz? Prueba a ejecutar la función dim().
dim(datos_matriz)## [1] 7 3Fíjate que dim() devuelve un vector de 2 elementos (las dos dimensiones), por lo que para acceder al número de filas deberemos ejecutar dim(x)[1] (y dim(x)[2] para el número de columnas).
dim(datos_matriz)[1]## [1] 7
dim(datos_matriz)[2]## [1] 3También tenemos a nuestra disposición las funciones nrow() y ncol(), que nos devuelven directamente el número de filas y columnas.
nrow(datos_matriz)## [1] 7
ncol(datos_matriz)## [1] 3Igual que a veces es útil generar un vector de elementos repetidos, también podemos definir una matriz de números repetidos (por ejemplo, de ceros), con la función matrix(), indicándole el número de filas y columnas.
matrix(0, nrow = 5, ncol = 3) # 5 filas, 3 columnas, todo 0's## [,1] [,2] [,3]
## [1,] 0 0 0
## [2,] 0 0 0
## [3,] 0 0 0
## [4,] 0 0 0
## [5,] 0 0 0También podemos definir una matriz a partir de un vector numérico, reorganizando los valores en forma de matriz (con una dimensión tal que filas * columnas = longitud del vector), sabiendo que los elementos se van colocando por columnas (primeros valores en la primera columna, de arriba a abajo).
z <- matrix(1:15, ncol = 5) # Matriz con el vector 1:5 con 5 columnas (ergo 3 filas)
z## [,1] [,2] [,3] [,4] [,5]
## [1,] 1 4 7 10 13
## [2,] 2 5 8 11 14
## [3,] 3 6 9 12 15
Dada una matriz también podemos «darle vuelta» (lo que se conoce como matriz transpuesta, donde filas pasan a ser columnas y viceversa) con la función t().
datos_matriz## edades tlf cp
## [1,] 14 NA 33007
## [2,] 24 683839390 28019
## [3,] 56 621539732 37005
## [4,] 31 618211286 18003
## [5,] 20 NA 33091
## [6,] 87 914727164 25073
## [7,] 73 NA 17140
t(datos_matriz) # Matriz transpuesta## [,1] [,2] [,3] [,4] [,5] [,6] [,7]
## edades 14 24 56 31 20 87 73
## tlf NA 683839390 621539732 618211286 NA 914727164 NA
## cp 33007 28019 37005 18003 33091 25073 17140Con las matrices sucede como con los vectores: cuando aplicamos una operación aritmética, se la estamos aplicando elemento a elemento, por ejemplo, dividir entre 5 o sumar una constante
datos_matriz / 5## edades tlf cp
## [1,] 2.8 NA 6601.4
## [2,] 4.8 136767878 5603.8
## [3,] 11.2 124307946 7401.0
## [4,] 6.2 123642257 3600.6
## [5,] 4.0 NA 6618.2
## [6,] 17.4 182945433 5014.6
## [7,] 14.6 NA 3428.0
datos_matriz + 3## edades tlf cp
## [1,] 17 NA 33010
## [2,] 27 683839393 28022
## [3,] 59 621539735 37008
## [4,] 34 618211289 18006
## [5,] 23 NA 33094
## [6,] 90 914727167 25076
## [7,] 76 NA 17143También podemos crear matrices de otros tipos de datos, siempre y cuando las columnas sean del mismo tipo e igual longitud, por ejemplo una matriz de caracteres o una matriz de valores lógicos
# matriz de caracteres
nombres <- c("Javier", "Carlos", "María", "Paloma")
apellidos <- c("Álvarez", "García", "Pérez", "Liébana")
cbind(nombres, apellidos)## nombres apellidos
## [1,] "Javier" "Álvarez"
## [2,] "Carlos" "García"
## [3,] "María" "Pérez"
## [4,] "Paloma" "Liébana"
# matriz de valores lógicos
var1 <- c(TRUE, TRUE, FALSE, FALSE, TRUE)
var2 <- c(TRUE, FALSE, FALSE, TRUE, TRUE)
cbind(var1, var2)## var1 var2
## [1,] TRUE TRUE
## [2,] TRUE FALSE
## [3,] FALSE FALSE
## [4,] FALSE TRUE
## [5,] TRUE TRUE
cbind(var1, var2) + 1## var1 var2
## [1,] 2 2
## [2,] 2 1
## [3,] 1 1
## [4,] 1 2
## [5,] 2 29.1.1 Acceder a elementos
Si recuerdas para los vectores, usábamos el operador [i] para acceder al elemento i-ésimo.
x <- c(1, 2, 10, 67, -1, 0)
x[3] # accedemos al tercer elemento ## [1] 10
x[c(3, 5)] # accedemos al tercer y quinto elemento## [1] 10 -1
x[1:4] # accedemos al primero, segundo, tercero, cuarto elemento## [1] 1 2 10 67En el caso de las matrices la lógica será la misma: para acceder a la fila i-ésima de la matriz se usa el operador [i, ] (dejando libre el índice de la columna), mientras que para acceder a la columna j-ésima de la matriz se usaría el operador [, j] (dejando libre el índice de la fila). Para acceder conjuntamente al elemento (i, j) (fila i, columna j) se usa el operador [i, j].
datos_matriz## edades tlf cp
## [1,] 14 NA 33007
## [2,] 24 683839390 28019
## [3,] 56 621539732 37005
## [4,] 31 618211286 18003
## [5,] 20 NA 33091
## [6,] 87 914727164 25073
## [7,] 73 NA 17140
datos_matriz[1, 3] # elemento (1, 3)## cp
## 33007
datos_matriz[2, 2] # elemento (1, 3)## tlf
## 683839390
datos_matriz[1, ] # fila 1## edades tlf cp
## 14 NA 33007
datos_matriz[, 3] # columna 3## [1] 33007 28019 37005 18003 33091 25073 17140Si las columnas tienen nombres también podemos hacer uso de ellos para acceder a las columnas
datos_matriz[, c("edades", "tlf")]## edades tlf
## [1,] 14 NA
## [2,] 24 683839390
## [3,] 56 621539732
## [4,] 31 618211286
## [5,] 20 NA
## [6,] 87 914727164
## [7,] 73 NAIncluso podemos asignar nombres a las filas de una matriz con row.names() y acceder a filas y columnas por nombres.
row.names(datos_matriz) <- c("Javi", "Laura", "Patricia", "Carlos",
"Juan", "Luis", "Carla")
datos_matriz["Javi", "edades"]## [1] 149.1.2 Operaciones por filas y columnas (apply)
Normalmente, para explicar las operaciones con matrices en un lenguaje de programación al uso, necesitaríamos hablar de una herramienta llamada bucles. Lo mencionaremos más adelante pero no los vamos a necesitar de momento (y cuántos menos los usemos en R, mejor)
Imagina que tuviésemos nuestra matriz de estaturas y pesos.
datos_matriz <- cbind(estaturas, pesos)
datos_matriz## estaturas pesos
## [1,] 150 60
## [2,] 160 70
## [3,] 170 80
## [4,] 180 90
## [5,] 190 100¿Cómo podemos aplicar una operación para cada una de las filas o columnas de una matriz? Imagina que queremos obtener la media de cada columna (media de las estaturas y media de los pesos).
Lo haremos con la función apply(), y le indicaremos como argumentos
- la matriz
- el sentido de la operación (
MARGIN = 1hará la opearción por filas,MARGIN = 2hará la opearción por columnas) - la función a aplicar por filas (o por columnas)
# Media (mean) por columnas (MARGIN = 2)
apply(datos_matriz, MARGIN = 2, FUN = "mean")## estaturas pesos
## 170 80El resultado es un vector de longitud 2 (la media de las estaturas y la media del peso). La misma operación la podemos realizar por filas con MARGIN = 1 (aunque en este caso no tiene mucho sentido hacer la media de variables con magnitudes distintas)
# Media por filas (MARGIN = 1)
apply(datos_matriz, MARGIN = 1, FUN = "mean")## [1] 105 115 125 135 145Si la función a aplicar requiere de argumentos extras, por ejemplo indicarle que ignore los datos ausentes con na.rm = TRUE, se lo podemos indicar al final como argumento extra.
estaturas_bis <- c(150, NA, 170, 180, 190)
pesos_bis <- c(60, 70, 80, NA, 100)
datos_matriz_bis <- cbind(estaturas_bis, pesos_bis)
# Nos devolverá ausente porque en ambas columnas tenemos
apply(datos_matriz_bis, MARGIN = 2, FUN = "mean")## estaturas_bis pesos_bis
## NA NA
# Media por columnas (MARGIN = 2) ignorando los ausentes
apply(datos_matriz_bis, MARGIN = 2, FUN = "mean", na.rm = TRUE)## estaturas_bis pesos_bis
## 172.5 77.59.2 Tablas: data.frames
Recapitulando:
- Hemos visto los tipos de datos que podemos tener en cada celda.
- Hemos aprendido a recolectar datos de distintos individuos (vectores de edades, vectores de fechas, vectores de nombres).
- Siempre que sean del mismo tipo y longitud, hemos aprendido a juntar en un mismo objeto (matrices) variables distintas (edades, estaturas, alturas, por ejemplo).
Retomemos nuestra matriz de datos, en la que teníamos para cada individuo guardado las edades (edades), teléfonos (tlf) y códigos postales (cp), y probemos a ver que pasa cuando seleccionamos la columna de edades y le sumamos un año a todas las personas
datos_matriz## estaturas pesos
## [1,] 150 60
## [2,] 160 70
## [3,] 170 80
## [4,] 180 90
## [5,] 190 100
# Sumamos un año a todas las personas
datos_matriz[, "pesos"] + 1## [1] 61 71 81 91 101¿Qué sucede si ahora añadimos una columna con los nombres (tipo caracter) de cada persona?
nombres <- c("Sonia", "Carla", "Pepito", "Carlos", "Lara", "Sandra", "Javi")
datos_matriz_nueva <- cbind(nombres, datos_matriz)¿Has visto lo que ha sucedido?
Como una matriz SOLO puede tener un tipo de dato (todo números, todo texto, todo lógicas, todo fechas, etc), al añadir una variable de tipo texto, R se ha visto obligado a convertir los números en texto poniéndole comillas a los datos que tenemos: hemos roto la integridad de los datos. De hecho, como ahora los números con caracteres, no podremos sumar un año a cada persona como antes.
datos_matriz_nueva[, "edades"] + 1## Error in datos_matriz_nueva[, "edades"]: subíndice fuera de los límites
Las matrices nos permiten almacenar distintas variables SIEMPRE Y CUANDO tengan
- Misma longitud (todas las columnas deben tener la misma longitud).
- Mismo tipo de dato (o todo números o todo caracteres, pero sin mezclar).
Esto es bastante limitante ya que en la vida real nuestros datos tendrán variables de todo tipo. Veamos un ejemplo real: supongamos que queremos guardar de 7 personas las variables de texto nombres y apellidos.
# Nombres
nombres <- c("Sonia", "Carla", "Pepito", "Carlos", "Lara", "Sandra", "Javi")
# Apellidos
apellidos <- c(NA, "González", "Fernández", "Martínez", "Liébana", "García", "Ortiz")Hasta aquí no habría ningún problema ya que podemos crear una matriz de caracteres.
matriz <- cbind(nombres, apellidos)
matriz## nombres apellidos
## [1,] "Sonia" NA
## [2,] "Carla" "González"
## [3,] "Pepito" "Fernández"
## [4,] "Carlos" "Martínez"
## [5,] "Lara" "Liébana"
## [6,] "Sandra" "García"
## [7,] "Javi" "Ortiz"De esas 7 personas también disponemos información de si están o no casadas (representado en un valor lógico, casado) y algunos valores numéricos (edades, cp y tlf).
# Código postal
cp <- c(28019, 28001, 34005, 18410, 33007, 34500, 28017)
# Edades
edades <- c(45, 67, NA, 31, 27, 19, 50)
# Teléfono
tlf <- c(618910564, 914718475, 934567891, 620176565, NA, NA, 688921344)
# Estado civil (no lo sabemos de una persona)
casado <- c(TRUE, FALSE, FALSE, NA, TRUE, FALSE, FALSE)Por último, vamos a añadir a cada persona una fecha de registro en el sistema (fecha_creacion, imagina que fuese la fecha de expedición del DNI).
# Fecha de creación (fecha en el que esa persona entra en el sistema)
# lo convertimos a tipo fecha
fecha_creacion <-
as_date(c("2021-03-04", "2020-10-12", "1990-04-05",
"2019-09-10", "2017-03-21", "2020-07-07",
"2000-01-28"))En cada variable tenemos 7 registros, uno por persona, pero ahora tenemos un popurrí de variables, de la misma longitud pero de tipos distintos:
-
(edades, tlf, cp)son variables numéricas. -
(nombres, apellidos)son variables de texto. -
casadoes una variable lógica. -
fecha_creacionde tipo fecha.
¿Qué sucedería si intentamos mezclar todo en una matriz? Vamos a unir las columnas con cbind().
# Juntamos todo en una matriz (juntamos por columnas)
datos_matriz <-
cbind(nombres, apellidos, edades, tlf, cp, casado, fecha_creacion)
datos_matriz## nombres apellidos edades tlf cp casado fecha_creacion
## [1,] "Sonia" NA "45" "618910564" "28019" "TRUE" "18690"
## [2,] "Carla" "González" "67" "914718475" "28001" "FALSE" "18547"
## [3,] "Pepito" "Fernández" NA "934567891" "34005" "FALSE" "7399"
## [4,] "Carlos" "Martínez" "31" "620176565" "18410" NA "18149"
## [5,] "Lara" "Liébana" "27" NA "33007" "TRUE" "17246"
## [6,] "Sandra" "García" "19" NA "34500" "FALSE" "18450"
## [7,] "Javi" "Ortiz" "50" "688921344" "28017" "FALSE" "10984"Dado que en una matriz solo podemos almacenar datos del mismo tipo, los números los convierte a texto, las variables lógicas las convierte a texto (TRUE ahora es un valor lógico, "TRUE" es un texto, como "Pepito", sin significado lógico de verdadero/falso) y las fechas las ha convertido a texto (aunque las veas igual, ya no son de tipo de fecha, son texto y no podemos operar con ellas).
# Días entre la primera y el segundo elemento de fecha de creación
fecha_creacion[1] - fecha_creacion[2]## Time difference of 143 days
datos_matriz[1, 7] - datos_matriz[2, 7]## Error in datos_matriz[1, 7] - datos_matriz[2, 7]: argumento no-numérico para operador binario
Vamos a aprender cómo juntar variables de distinto tipo, sin cambiar su naturaleza, como lo haríamos en una tabla de Excel.
El formato de tabla de datos en R que vamos a empezar a usar desde ya se llama data.frame, y no es más que una colección de variables de igual longitud pero cada una puede ser de un tipo distinto. Para crear un data.frame basta con usar la función data.frame(), pasándole como argumentos (separados por comas) las variables que queremos reunir.
# Creamos nuestro primer data.frame
tabla <- data.frame(nombres, apellidos, edades, tlf, cp,
casado, fecha_creacion)
tabla## nombres apellidos edades tlf cp casado fecha_creacion
## 1 Sonia <NA> 45 618910564 28019 TRUE 2021-03-04
## 2 Carla González 67 914718475 28001 FALSE 2020-10-12
## 3 Pepito Fernández NA 934567891 34005 FALSE 1990-04-05
## 4 Carlos Martínez 31 620176565 18410 NA 2019-09-10
## 5 Lara Liébana 27 NA 33007 TRUE 2017-03-21
## 6 Sandra García 19 NA 34500 FALSE 2020-07-07
## 7 Javi Ortiz 50 688921344 28017 FALSE 2000-01-28
class(tabla)## [1] "data.frame"Al igual que con las matrices, podemos crearlas indicando además el nombre de las columnas.
tabla <- data.frame("nombre" = nombres, "apellido" = apellidos,
"edad" = edades, "teléfono" = tlf,
"cp" = cp, "casado" = casado,
"fecha_registro" = fecha_creacion)
tabla## nombre apellido edad teléfono cp casado fecha_registro
## 1 Sonia <NA> 45 618910564 28019 TRUE 2021-03-04
## 2 Carla González 67 914718475 28001 FALSE 2020-10-12
## 3 Pepito Fernández NA 934567891 34005 FALSE 1990-04-05
## 4 Carlos Martínez 31 620176565 18410 NA 2019-09-10
## 5 Lara Liébana 27 NA 33007 TRUE 2017-03-21
## 6 Sandra García 19 NA 34500 FALSE 2020-07-07
## 7 Javi Ortiz 50 688921344 28017 FALSE 2000-01-28¡TENEMOS NUESTRO PRIMER CONJUNTO DE DATOS! Puedes visualizarlo de nuevo escribiendo su nombre en consola o con la función View()
View(tabla)9.2.1 Selección de columnas y filas
Si tenemos un data.frame ya creado y queremos añadir una columna es tan simple como usar la función data.frame() que ya hemos visto para concatenar la columna. Vamos añadir por ejemplo una nueva variable, el número de hermanos de cada individuo.
# Añadimos una nueva columna con nº de hermanos/as
hermanos <- c(0, 0, 1, 5, 2, 3, 0)
tabla <- data.frame(tabla, "n_hermanos" = hermanos)
tabla## nombre apellido edad teléfono cp casado fecha_registro n_hermanos
## 1 Sonia <NA> 45 618910564 28019 TRUE 2021-03-04 0
## 2 Carla González 67 914718475 28001 FALSE 2020-10-12 0
## 3 Pepito Fernández NA 934567891 34005 FALSE 1990-04-05 1
## 4 Carlos Martínez 31 620176565 18410 NA 2019-09-10 5
## 5 Lara Liébana 27 NA 33007 TRUE 2017-03-21 2
## 6 Sandra García 19 NA 34500 FALSE 2020-07-07 3
## 7 Javi Ortiz 50 688921344 28017 FALSE 2000-01-28 0Si queremos acceder a una columna, fila o elemento en concreto, los data.frame tienen las mismas ventajas que una matriz, así que bastaría con usar los mismos operadores.
tabla[, 3] # Accedemos a la tercera columna## [1] 45 67 NA 31 27 19 50
tabla[5, ] # Accedemos a la quinta fila## nombre apellido edad teléfono cp casado fecha_registro n_hermanos
## 5 Lara Liébana 27 NA 33007 TRUE 2017-03-21 2
tabla[5, 3] # Accedemos a la tercera variable del quinto registro## [1] 27Un data.frame no solo tiene las ventajas de una matriz si no que también tiene las ventajas de una «base» de datos. Por ejemplo, podemos aceder a las variables por el índice de columna que ocupan pero también acceder a las columnas por su nombre, poniendo el nombre de la tabla, el símbolo $ y, con el tabulador, nos aparecerá un menú de columnas a elegir.
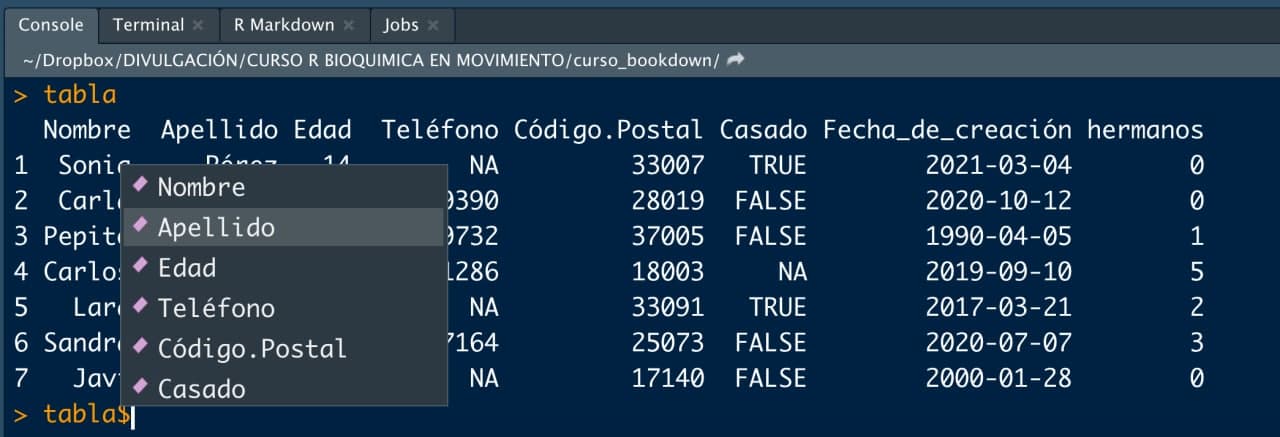
Imagen/gráfica 9.2: Menú desplegable de variables (columnas) de un data.frame.
9.2.2 Primer análisis de datos: arrestos en EE. UU.
Además del conjunto de datos tabla que hemos construido artificialmente, vamos a instalar (sino lo hemos hecho nunca en este ordenador) un paquete muy útil en R llamado {datasets}.
# Paquetes necesarios
# install.packages("datasets") # Descomentar si nunca se ha instalado
library(datasets)Ahora si escribimos datasets:: y pulsamos tabulador, se nos abre un desplegable con distintos conjuntos de datos reales para ser usados: el paquete datasets nos proporciona data.frames de prueba para que podamos usarlos.
Vamos a jugar con el conjunto de datos datasets::USArrests, que contiene estadísticas de arrestos en 1973 (por cada 100 000 habitantes) por agresión, asesinato y violación, en cada uno de los 50 estados de Estaods Unidos.
¿Cómo visualizar la cabecera de la tabla? Con la función head().
head(USArrests)## Murder Assault UrbanPop Rape
## Alabama 13.2 236 58 21.2
## Alaska 10.0 263 48 44.5
## Arizona 8.1 294 80 31.0
## Arkansas 8.8 190 50 19.5
## California 9.0 276 91 40.6
## Colorado 7.9 204 78 38.7¿Cómo obtener el nombre de las variables? Con la función names().
names(USArrests)## [1] "Murder" "Assault" "UrbanPop" "Rape"El conjunto contiene los 3 tipos de delito mencionados (para cada estado), y además el porcentaje de población que vive en áreas urbanas. Esto lo podemos saber ejecutando la ayuda con ? datasets::USArrests.
¿Cómo obtener el nombre de las filas (de los estados)? Con la función row.names().
row.names(USArrests)## [1] "Alabama" "Alaska" "Arizona" "Arkansas"
## [5] "California" "Colorado" "Connecticut" "Delaware"
## [9] "Florida" "Georgia" "Hawaii" "Idaho"
## [13] "Illinois" "Indiana" "Iowa" "Kansas"
## [17] "Kentucky" "Louisiana" "Maine" "Maryland"
## [21] "Massachusetts" "Michigan" "Minnesota" "Mississippi"
## [25] "Missouri" "Montana" "Nebraska" "Nevada"
## [29] "New Hampshire" "New Jersey" "New Mexico" "New York"
## [33] "North Carolina" "North Dakota" "Ohio" "Oklahoma"
## [37] "Oregon" "Pennsylvania" "Rhode Island" "South Carolina"
## [41] "South Dakota" "Tennessee" "Texas" "Utah"
## [45] "Vermont" "Virginia" "Washington" "West Virginia"
## [49] "Wisconsin" "Wyoming"¿Cómo averiguar el número de registros y el número de variables? Con las funciones dim(), nrow() y ncol().
dim(USArrests)## [1] 50 4
nrow(USArrests)## [1] 50
ncol(USArrests)## [1] 4¿Cómo seleccionar solo las columnas Murder y Assault para el segundo y el décimo estado?
## Murder Assault
## Alaska 10.0 263
## Georgia 17.4 211
¿Cómo cambiar el nombre de las variables? Con la función names().
¿Cómo seleccionar y filtrar datos?
En el caso de los data.frame tenemos además a nuestro disposición una herramienta muy potente: la función subset(). Dicha función nos va a permitir seleccionar filas y columnas a la vez, tomando de entrada los siguientes argumentos
-
x: una tabla de entrada, undata.framede entrada. -
subset: la condición lógica que queramos usar para seleccionar registros (filas). -
select: un vector que contenga el nombre de las columnas que queremos seleccionar (a lo mejor solo queremos filtrar por filas pero quizás también por columnas).
Por ejemplo, vamos a seleccionar solo los delitos de asesinato de aquellos estados cuyo porcentaje de población urbana sea superior al 70%.
## asesinato
## Arizona 8.1
## California 9.0
## Colorado 7.9
## Connecticut 3.3
## Delaware 5.9
## Florida 15.4
## Hawaii 5.3
## Illinois 10.4
## Massachusetts 4.4
## Michigan 12.1
## Nevada 12.2
## New Jersey 7.4
## New York 11.1
## Ohio 7.3
## Pennsylvania 6.3
## Rhode Island 3.4
## Texas 12.7
## Utah 3.2
## Washington 4.0Como sucedía en otros contextos, podemos combinar condiciones lógicas, seleccionando por ejemplo aquellos estados cuyo porcentaje de población urbana sea inferior al 70% y donde las agresiones sean superiores a 250 por cada 100 000 habitantes, pero luego seleccionando solo dos variables.
## asesinato violacion
## Alaska 10.0 44.5
## Maryland 11.3 27.8
## Mississippi 16.1 17.1
## North Carolina 13.0 16.1
## South Carolina 14.4 22.59.3 Consejos
CONSEJOS
Acceder a las funciones de los paquetes
A veces puede que no queramos cargar todo un paquete sino solo una función del mismo, para lo que es suficiente nombre_paquete::nombre_funcion. Recuerda que instalar un paquete es cómo comprar un libro, cargar el paquete con library() es cómo traer el libro comprado de la estantería a tu mesa, y usar solo una función con nombre_paquete::nombre_funcion es cómo pedirle a alguien que te arranque solo una página y te la traiga a la mesa.
9.4 📝 Ejercicios
(haz click en las flechas para ver soluciones)
Ejercicio 1: modifica el código para definir una matriz
x de ceros de 3 filas y 7 columnas.
- Solución:
# Matriz
x <- matrix(0, nrow = 3, ncol = 7)
x## [,1] [,2] [,3] [,4] [,5] [,6] [,7]
## [1,] 0 0 0 0 0 0 0
## [2,] 0 0 0 0 0 0 0
## [3,] 0 0 0 0 0 0 0
# Matriz
x <- matrix(0, nrow = 2, ncol = 3)
x
Ejercicio 2: a la matriz anterior, suma un 1 a cada número de la matriz y divide el resultado entre 5.
- Solución:
(x + 1) / 5## [,1] [,2] [,3] [,4] [,5] [,6] [,7]
## [1,] 0.2 0.2 0.2 0.2 0.2 0.2 0.2
## [2,] 0.2 0.2 0.2 0.2 0.2 0.2 0.2
## [3,] 0.2 0.2 0.2 0.2 0.2 0.2 0.2
Ejercicio 3: tras definir la matriz
x calcula su transpuesta y obtén sus dimensiones
- Solución:
# Transpuesta
t(x)## [,1] [,2] [,3]
## [1,] 0 0 0
## [2,] 0 0 0
## [3,] 0 0 0
## [4,] 0 0 0
## [5,] 0 0 0
## [6,] 0 0 0
## [7,] 0 0 0## [1] 7 3## [1] 3## [1] 7
Ejercicio 4: el siguiente código define una matriz de dimensiones
4 x 3 y calcula la suma por columnas. Modifica el código para que realice la suma por filas.
- Solución:
## [1] 15 18 21 24
# Matriz
matriz <- matrix(1:12, nrow = 4)
# Suma por columnas
apply(matriz, MARGIN = 2, FUN = "sum")## [1] 10 26 42
Ejercicio 5: con la matriz anterior definida como
matrix(1:12, nrow = 4), calcula la media de todos los elementos, la media de cada fila y la media de cada columna.
- Solución:
## [1] 6.5
# Media por filas (MARGIN = 1 ya que es una operación por filas)
apply(matriz, MARGIN = 1, FUN = "mean")## [1] 5 6 7 8
# Media por filas (MARGIN = 2 ya que es una operación por filas)
apply(matriz, MARGIN = 2, FUN = "mean")## [1] 2.5 6.5 10.5
Ejercicio 6: el
data.frame llamado airquality, del paquete {datasets}, contiene variables de la calidad del aire de la ciudad de Nueva York desde mayo hasta septiembre de 1973. Obtén el nombre de las variables.
- Solución:
## [1] "Ozone" "Solar.R" "Wind" "Temp" "Month" "Day"
Ejercicio 7: obtén las dimensiones del conjunto de datos. ¿Cuántas variables hay? ¿Cuántos días se han medido?
- Solución:
# Dimensiones
dim(airquality)## [1] 153 6
nrow(airquality)## [1] 153
ncol(airquality)## [1] 6
Ejercicio 8: modifica el código inferior para que nos filtre solo los datos del mes de julio.
- Solución:
# Filtramos filas
filtro_fila <- subset(airquality, subset = Month == 7)
filtro_fila## Ozone Solar.R Wind Temp Month Day
## 62 135 269 4.1 84 7 1
## 63 49 248 9.2 85 7 2
## 64 32 236 9.2 81 7 3
## 65 NA 101 10.9 84 7 4
## 66 64 175 4.6 83 7 5
## 67 40 314 10.9 83 7 6
## 68 77 276 5.1 88 7 7
## 69 97 267 6.3 92 7 8
## 70 97 272 5.7 92 7 9
## 71 85 175 7.4 89 7 10
## 72 NA 139 8.6 82 7 11
## 73 10 264 14.3 73 7 12
## 74 27 175 14.9 81 7 13
## 75 NA 291 14.9 91 7 14
## 76 7 48 14.3 80 7 15
## 77 48 260 6.9 81 7 16
## 78 35 274 10.3 82 7 17
## 79 61 285 6.3 84 7 18
## 80 79 187 5.1 87 7 19
## 81 63 220 11.5 85 7 20
## 82 16 7 6.9 74 7 21
## 83 NA 258 9.7 81 7 22
## 84 NA 295 11.5 82 7 23
## 85 80 294 8.6 86 7 24
## 86 108 223 8.0 85 7 25
## 87 20 81 8.6 82 7 26
## 88 52 82 12.0 86 7 27
## 89 82 213 7.4 88 7 28
## 90 50 275 7.4 86 7 29
## 91 64 253 7.4 83 7 30
## 92 59 254 9.2 81 7 31
# Filtramos filas
filtro_fila <- subset(., subset = Month < 6)
filtro_fila
Ejercicio 9: del conjunto
airquality selecciona aquellos datos que no sean ni de julio ni de agosto.
- Solución:
## Ozone Solar.R Wind Temp Month Day
## 1 41 190 7.4 67 5 1
## 2 36 118 8.0 72 5 2
## 3 12 149 12.6 74 5 3
## 4 18 313 11.5 62 5 4
## 5 NA NA 14.3 56 5 5
## 6 28 NA 14.9 66 5 6
## 7 23 299 8.6 65 5 7
## 8 19 99 13.8 59 5 8
## 9 8 19 20.1 61 5 9
## 10 NA 194 8.6 69 5 10
## 11 7 NA 6.9 74 5 11
## 12 16 256 9.7 69 5 12
## 13 11 290 9.2 66 5 13
## 14 14 274 10.9 68 5 14
## 15 18 65 13.2 58 5 15
## 16 14 334 11.5 64 5 16
## 17 34 307 12.0 66 5 17
## 18 6 78 18.4 57 5 18
## 19 30 322 11.5 68 5 19
## 20 11 44 9.7 62 5 20
## 21 1 8 9.7 59 5 21
## 22 11 320 16.6 73 5 22
## 23 4 25 9.7 61 5 23
## 24 32 92 12.0 61 5 24
## 25 NA 66 16.6 57 5 25
## 26 NA 266 14.9 58 5 26
## 27 NA NA 8.0 57 5 27
## 28 23 13 12.0 67 5 28
## 29 45 252 14.9 81 5 29
## 30 115 223 5.7 79 5 30
## 31 37 279 7.4 76 5 31
## 32 NA 286 8.6 78 6 1
## 33 NA 287 9.7 74 6 2
## 34 NA 242 16.1 67 6 3
## 35 NA 186 9.2 84 6 4
## 36 NA 220 8.6 85 6 5
## 37 NA 264 14.3 79 6 6
## 38 29 127 9.7 82 6 7
## 39 NA 273 6.9 87 6 8
## 40 71 291 13.8 90 6 9
## 41 39 323 11.5 87 6 10
## 42 NA 259 10.9 93 6 11
## 43 NA 250 9.2 92 6 12
## 44 23 148 8.0 82 6 13
## 45 NA 332 13.8 80 6 14
## 46 NA 322 11.5 79 6 15
## 47 21 191 14.9 77 6 16
## 48 37 284 20.7 72 6 17
## 49 20 37 9.2 65 6 18
## 50 12 120 11.5 73 6 19
## 51 13 137 10.3 76 6 20
## 52 NA 150 6.3 77 6 21
## 53 NA 59 1.7 76 6 22
## 54 NA 91 4.6 76 6 23
## 55 NA 250 6.3 76 6 24
## 56 NA 135 8.0 75 6 25
## 57 NA 127 8.0 78 6 26
## 58 NA 47 10.3 73 6 27
## 59 NA 98 11.5 80 6 28
## 60 NA 31 14.9 77 6 29
## 61 NA 138 8.0 83 6 30
## 124 96 167 6.9 91 9 1
## 125 78 197 5.1 92 9 2
## 126 73 183 2.8 93 9 3
## 127 91 189 4.6 93 9 4
## 128 47 95 7.4 87 9 5
## 129 32 92 15.5 84 9 6
## 130 20 252 10.9 80 9 7
## 131 23 220 10.3 78 9 8
## 132 21 230 10.9 75 9 9
## 133 24 259 9.7 73 9 10
## 134 44 236 14.9 81 9 11
## 135 21 259 15.5 76 9 12
## 136 28 238 6.3 77 9 13
## 137 9 24 10.9 71 9 14
## 138 13 112 11.5 71 9 15
## 139 46 237 6.9 78 9 16
## 140 18 224 13.8 67 9 17
## 141 13 27 10.3 76 9 18
## 142 24 238 10.3 68 9 19
## 143 16 201 8.0 82 9 20
## 144 13 238 12.6 64 9 21
## 145 23 14 9.2 71 9 22
## 146 36 139 10.3 81 9 23
## 147 7 49 10.3 69 9 24
## 148 14 20 16.6 63 9 25
## 149 30 193 6.9 70 9 26
## 150 NA 145 13.2 77 9 27
## 151 14 191 14.3 75 9 28
## 152 18 131 8.0 76 9 29
## 153 20 223 11.5 68 9 30
Ejercicio 10: modifica el siguiente código para quedarte solo con las variable
Ozone y Temp.
- Solución:
## Ozone Temp
## 1 41 67
## 2 36 72
## 3 12 74
## 4 18 62
## 5 NA 56
## 6 28 66
## 7 23 65
## 8 19 59
## 9 8 61
## 10 NA 69
## 11 7 74
## 12 16 69
## 13 11 66
## 14 14 68
## 15 18 58
## 16 14 64
## 17 34 66
## 18 6 57
## 19 30 68
## 20 11 62
## 21 1 59
## 22 11 73
## 23 4 61
## 24 32 61
## 25 NA 57
## 26 NA 58
## 27 NA 57
## 28 23 67
## 29 45 81
## 30 115 79
## 31 37 76
## 32 NA 78
## 33 NA 74
## 34 NA 67
## 35 NA 84
## 36 NA 85
## 37 NA 79
## 38 29 82
## 39 NA 87
## 40 71 90
## 41 39 87
## 42 NA 93
## 43 NA 92
## 44 23 82
## 45 NA 80
## 46 NA 79
## 47 21 77
## 48 37 72
## 49 20 65
## 50 12 73
## 51 13 76
## 52 NA 77
## 53 NA 76
## 54 NA 76
## 55 NA 76
## 56 NA 75
## 57 NA 78
## 58 NA 73
## 59 NA 80
## 60 NA 77
## 61 NA 83
## 62 135 84
## 63 49 85
## 64 32 81
## 65 NA 84
## 66 64 83
## 67 40 83
## 68 77 88
## 69 97 92
## 70 97 92
## 71 85 89
## 72 NA 82
## 73 10 73
## 74 27 81
## 75 NA 91
## 76 7 80
## 77 48 81
## 78 35 82
## 79 61 84
## 80 79 87
## 81 63 85
## 82 16 74
## 83 NA 81
## 84 NA 82
## 85 80 86
## 86 108 85
## 87 20 82
## 88 52 86
## 89 82 88
## 90 50 86
## 91 64 83
## 92 59 81
## 93 39 81
## 94 9 81
## 95 16 82
## 96 78 86
## 97 35 85
## 98 66 87
## 99 122 89
## 100 89 90
## 101 110 90
## 102 NA 92
## 103 NA 86
## 104 44 86
## 105 28 82
## 106 65 80
## 107 NA 79
## 108 22 77
## 109 59 79
## 110 23 76
## 111 31 78
## 112 44 78
## 113 21 77
## 114 9 72
## 115 NA 75
## 116 45 79
## 117 168 81
## 118 73 86
## 119 NA 88
## 120 76 97
## 121 118 94
## 122 84 96
## 123 85 94
## 124 96 91
## 125 78 92
## 126 73 93
## 127 91 93
## 128 47 87
## 129 32 84
## 130 20 80
## 131 23 78
## 132 21 75
## 133 24 73
## 134 44 81
## 135 21 76
## 136 28 77
## 137 9 71
## 138 13 71
## 139 46 78
## 140 18 67
## 141 13 76
## 142 24 68
## 143 16 82
## 144 13 64
## 145 23 71
## 146 36 81
## 147 7 69
## 148 14 63
## 149 30 70
## 150 NA 77
## 151 14 75
## 152 18 76
## 153 20 68
Ejercicio 11: del conjunto
airquality selecciona los datos de temperatura y viento de agosto.
- Solución:
# Todo de una vez
filtro <- subset(airquality, subset = Month == 8,
select = c("Temp", "Wind"))
filtro## Temp Wind
## 93 81 6.9
## 94 81 13.8
## 95 82 7.4
## 96 86 6.9
## 97 85 7.4
## 98 87 4.6
## 99 89 4.0
## 100 90 10.3
## 101 90 8.0
## 102 92 8.6
## 103 86 11.5
## 104 86 11.5
## 105 82 11.5
## 106 80 9.7
## 107 79 11.5
## 108 77 10.3
## 109 79 6.3
## 110 76 7.4
## 111 78 10.9
## 112 78 10.3
## 113 77 15.5
## 114 72 14.3
## 115 75 12.6
## 116 79 9.7
## 117 81 3.4
## 118 86 8.0
## 119 88 5.7
## 120 97 9.7
## 121 94 2.3
## 122 96 6.3
## 123 94 6.3
Ejercicio 12: calcula el número de filas borradas del ejercicio anterior. Tras hacer todo ello, traduce a castellano el nombre de las columnas del
data.frame filtrado.
- Solución:
## [1] 122
Ejercicio 13: añade a los datos originales una columna con la fecha completa (recuerda que es del año 1973 todas las observaciones.
- Solución:
# Construimos las fechas (pegamos año-mes-día con "-")
fechas <-
as_date(paste("1973", airquality$Month, airquality$Day,
sep = "-"))
# Añadimos
data.frame(airquality, fechas)## Ozone Solar.R Wind Temp Month Day fechas
## 1 41 190 7.4 67 5 1 1973-05-01
## 2 36 118 8.0 72 5 2 1973-05-02
## 3 12 149 12.6 74 5 3 1973-05-03
## 4 18 313 11.5 62 5 4 1973-05-04
## 5 NA NA 14.3 56 5 5 1973-05-05
## 6 28 NA 14.9 66 5 6 1973-05-06
## 7 23 299 8.6 65 5 7 1973-05-07
## 8 19 99 13.8 59 5 8 1973-05-08
## 9 8 19 20.1 61 5 9 1973-05-09
## 10 NA 194 8.6 69 5 10 1973-05-10
## 11 7 NA 6.9 74 5 11 1973-05-11
## 12 16 256 9.7 69 5 12 1973-05-12
## 13 11 290 9.2 66 5 13 1973-05-13
## 14 14 274 10.9 68 5 14 1973-05-14
## 15 18 65 13.2 58 5 15 1973-05-15
## 16 14 334 11.5 64 5 16 1973-05-16
## 17 34 307 12.0 66 5 17 1973-05-17
## 18 6 78 18.4 57 5 18 1973-05-18
## 19 30 322 11.5 68 5 19 1973-05-19
## 20 11 44 9.7 62 5 20 1973-05-20
## 21 1 8 9.7 59 5 21 1973-05-21
## 22 11 320 16.6 73 5 22 1973-05-22
## 23 4 25 9.7 61 5 23 1973-05-23
## 24 32 92 12.0 61 5 24 1973-05-24
## 25 NA 66 16.6 57 5 25 1973-05-25
## 26 NA 266 14.9 58 5 26 1973-05-26
## 27 NA NA 8.0 57 5 27 1973-05-27
## 28 23 13 12.0 67 5 28 1973-05-28
## 29 45 252 14.9 81 5 29 1973-05-29
## 30 115 223 5.7 79 5 30 1973-05-30
## 31 37 279 7.4 76 5 31 1973-05-31
## 32 NA 286 8.6 78 6 1 1973-06-01
## 33 NA 287 9.7 74 6 2 1973-06-02
## 34 NA 242 16.1 67 6 3 1973-06-03
## 35 NA 186 9.2 84 6 4 1973-06-04
## 36 NA 220 8.6 85 6 5 1973-06-05
## 37 NA 264 14.3 79 6 6 1973-06-06
## 38 29 127 9.7 82 6 7 1973-06-07
## 39 NA 273 6.9 87 6 8 1973-06-08
## 40 71 291 13.8 90 6 9 1973-06-09
## 41 39 323 11.5 87 6 10 1973-06-10
## 42 NA 259 10.9 93 6 11 1973-06-11
## 43 NA 250 9.2 92 6 12 1973-06-12
## 44 23 148 8.0 82 6 13 1973-06-13
## 45 NA 332 13.8 80 6 14 1973-06-14
## 46 NA 322 11.5 79 6 15 1973-06-15
## 47 21 191 14.9 77 6 16 1973-06-16
## 48 37 284 20.7 72 6 17 1973-06-17
## 49 20 37 9.2 65 6 18 1973-06-18
## 50 12 120 11.5 73 6 19 1973-06-19
## 51 13 137 10.3 76 6 20 1973-06-20
## 52 NA 150 6.3 77 6 21 1973-06-21
## 53 NA 59 1.7 76 6 22 1973-06-22
## 54 NA 91 4.6 76 6 23 1973-06-23
## 55 NA 250 6.3 76 6 24 1973-06-24
## 56 NA 135 8.0 75 6 25 1973-06-25
## 57 NA 127 8.0 78 6 26 1973-06-26
## 58 NA 47 10.3 73 6 27 1973-06-27
## 59 NA 98 11.5 80 6 28 1973-06-28
## 60 NA 31 14.9 77 6 29 1973-06-29
## 61 NA 138 8.0 83 6 30 1973-06-30
## 62 135 269 4.1 84 7 1 1973-07-01
## 63 49 248 9.2 85 7 2 1973-07-02
## 64 32 236 9.2 81 7 3 1973-07-03
## 65 NA 101 10.9 84 7 4 1973-07-04
## 66 64 175 4.6 83 7 5 1973-07-05
## 67 40 314 10.9 83 7 6 1973-07-06
## 68 77 276 5.1 88 7 7 1973-07-07
## 69 97 267 6.3 92 7 8 1973-07-08
## 70 97 272 5.7 92 7 9 1973-07-09
## 71 85 175 7.4 89 7 10 1973-07-10
## 72 NA 139 8.6 82 7 11 1973-07-11
## 73 10 264 14.3 73 7 12 1973-07-12
## 74 27 175 14.9 81 7 13 1973-07-13
## 75 NA 291 14.9 91 7 14 1973-07-14
## 76 7 48 14.3 80 7 15 1973-07-15
## 77 48 260 6.9 81 7 16 1973-07-16
## 78 35 274 10.3 82 7 17 1973-07-17
## 79 61 285 6.3 84 7 18 1973-07-18
## 80 79 187 5.1 87 7 19 1973-07-19
## 81 63 220 11.5 85 7 20 1973-07-20
## 82 16 7 6.9 74 7 21 1973-07-21
## 83 NA 258 9.7 81 7 22 1973-07-22
## 84 NA 295 11.5 82 7 23 1973-07-23
## 85 80 294 8.6 86 7 24 1973-07-24
## 86 108 223 8.0 85 7 25 1973-07-25
## 87 20 81 8.6 82 7 26 1973-07-26
## 88 52 82 12.0 86 7 27 1973-07-27
## 89 82 213 7.4 88 7 28 1973-07-28
## 90 50 275 7.4 86 7 29 1973-07-29
## 91 64 253 7.4 83 7 30 1973-07-30
## 92 59 254 9.2 81 7 31 1973-07-31
## 93 39 83 6.9 81 8 1 1973-08-01
## 94 9 24 13.8 81 8 2 1973-08-02
## 95 16 77 7.4 82 8 3 1973-08-03
## 96 78 NA 6.9 86 8 4 1973-08-04
## 97 35 NA 7.4 85 8 5 1973-08-05
## 98 66 NA 4.6 87 8 6 1973-08-06
## 99 122 255 4.0 89 8 7 1973-08-07
## 100 89 229 10.3 90 8 8 1973-08-08
## 101 110 207 8.0 90 8 9 1973-08-09
## 102 NA 222 8.6 92 8 10 1973-08-10
## 103 NA 137 11.5 86 8 11 1973-08-11
## 104 44 192 11.5 86 8 12 1973-08-12
## 105 28 273 11.5 82 8 13 1973-08-13
## 106 65 157 9.7 80 8 14 1973-08-14
## 107 NA 64 11.5 79 8 15 1973-08-15
## 108 22 71 10.3 77 8 16 1973-08-16
## 109 59 51 6.3 79 8 17 1973-08-17
## 110 23 115 7.4 76 8 18 1973-08-18
## 111 31 244 10.9 78 8 19 1973-08-19
## 112 44 190 10.3 78 8 20 1973-08-20
## 113 21 259 15.5 77 8 21 1973-08-21
## 114 9 36 14.3 72 8 22 1973-08-22
## 115 NA 255 12.6 75 8 23 1973-08-23
## 116 45 212 9.7 79 8 24 1973-08-24
## 117 168 238 3.4 81 8 25 1973-08-25
## 118 73 215 8.0 86 8 26 1973-08-26
## 119 NA 153 5.7 88 8 27 1973-08-27
## 120 76 203 9.7 97 8 28 1973-08-28
## 121 118 225 2.3 94 8 29 1973-08-29
## 122 84 237 6.3 96 8 30 1973-08-30
## 123 85 188 6.3 94 8 31 1973-08-31
## 124 96 167 6.9 91 9 1 1973-09-01
## 125 78 197 5.1 92 9 2 1973-09-02
## 126 73 183 2.8 93 9 3 1973-09-03
## 127 91 189 4.6 93 9 4 1973-09-04
## 128 47 95 7.4 87 9 5 1973-09-05
## 129 32 92 15.5 84 9 6 1973-09-06
## 130 20 252 10.9 80 9 7 1973-09-07
## 131 23 220 10.3 78 9 8 1973-09-08
## 132 21 230 10.9 75 9 9 1973-09-09
## 133 24 259 9.7 73 9 10 1973-09-10
## 134 44 236 14.9 81 9 11 1973-09-11
## 135 21 259 15.5 76 9 12 1973-09-12
## 136 28 238 6.3 77 9 13 1973-09-13
## 137 9 24 10.9 71 9 14 1973-09-14
## 138 13 112 11.5 71 9 15 1973-09-15
## 139 46 237 6.9 78 9 16 1973-09-16
## 140 18 224 13.8 67 9 17 1973-09-17
## 141 13 27 10.3 76 9 18 1973-09-18
## 142 24 238 10.3 68 9 19 1973-09-19
## 143 16 201 8.0 82 9 20 1973-09-20
## 144 13 238 12.6 64 9 21 1973-09-21
## 145 23 14 9.2 71 9 22 1973-09-22
## 146 36 139 10.3 81 9 23 1973-09-23
## 147 7 49 10.3 69 9 24 1973-09-24
## 148 14 20 16.6 63 9 25 1973-09-25
## 149 30 193 6.9 70 9 26 1973-09-26
## 150 NA 145 13.2 77 9 27 1973-09-27
## 151 14 191 14.3 75 9 28 1973-09-28
## 152 18 131 8.0 76 9 29 1973-09-29
## 153 20 223 11.5 68 9 30 1973-09-30