Capítulo 23 Extrayendo información: estadística descriptiva con cualitativas
Scripts usados:
- script23.R: intro a la descriptiva con cualitativas. Ver en https://github.com/dadosdelaplace/courses-ECI-2022/blob/main/scripts/script23.R
Como ya hemos comentado, algunas de las grandes fortalezas de R frente a Python están relacionadas con la disponibilidad de herramientas para generar informes y herramientas de visualización y procesamiento de datos. Pero si R es tan conocido en ciencias es por ser un lenguaje de programación sencillo para aplicar estadística y Machine Learning, con una inmensa cantidad de paquetes relacionados con ello. En este bloque vamos a introducirnos a la estadística descriptiva en varios niveles:
- Análisis univariante de variables categóricas: una sola variable que representa una categoría o cualidad.
- Análisis univariante de variables continuas: una sola variable que representa una variable cuantificable numéricamente.
- Análisis multivariante de distintos tipos de variables: varias variables a la vez
23.1 ¿Qué es la estadística descriptiva?
Una buena definición de estadística puede ser la encontrada en wikipedia:
La estadística (la forma femenina del término alemán Statistik, derivado a su vez del italiano statista, “hombre de Estado”), es la rama de la matemática que estudia la variabilidad, colección, organización, análisis, interpretación, y presentación de los datos, así como el proceso aleatorio que los genera siguiendo las leyes de la probabilidad.
La estadística descriptiva es la herramienta fundamental para obtener esa información, para obtener valor de los datos generados a partir de los sucesos de estudio mediante la descripción, visualización y agregación de los mismos.
23.1.1 Población y muestra
El uso primigenio de la estadística, y de donde deriva etimológicamente la palabra, es el estudio y organización del Estado, por lo que muchos términos hacen referencia a dicho origen. Vamos a introducir algunos términos usando como ejemplo el conjunto que ya conocemos de starwars, en el que tenemos datos de 87 personajes.
Población: el conjunto o colección de individuos a estudiar (por ejemplo, los cientos de miles de habitantes de los mundos de Star Wars). En general llamaremos población al conjunto de posibles elementos o eventos de los que podríamos tener observaciones. El problema es que esa población normalmente es inaccesible su totalidad (en el caso de obtener estadísticas de la estatura de toda la población española, sería inviable medir a los 47 millones de habitantes).
Individuo: cada uno de los elementos sobre los que vamos a medir una característica (normalmente las filas de una tabla)
Muestra: una selección «representativa» de la población total (teórica). En nuestro caso, de los miles de habitantes de los mundos de Star Wars hemos extraído una muestra de 87 personas. La rama de la estadística que se encarga del estudio de cómo obtener esas muestras, en función del objetivo que se tenga, se conoce como muestreo.
## # A tibble: 87 × 14
## name height mass hair_color skin_color eye_color birth_year sex gender
## <chr> <int> <dbl> <chr> <chr> <chr> <dbl> <chr> <chr>
## 1 Luke S… 172 77 blond fair blue 19 male mascu…
## 2 C-3PO 167 75 <NA> gold yellow 112 none mascu…
## 3 R2-D2 96 32 <NA> white, bl… red 33 none mascu…
## 4 Darth … 202 136 none white yellow 41.9 male mascu…
## 5 Leia O… 150 49 brown light brown 19 fema… femin…
## 6 Owen L… 178 120 brown, grey light blue 52 male mascu…
## 7 Beru W… 165 75 brown light blue 47 fema… femin…
## 8 R5-D4 97 32 <NA> white, red red NA none mascu…
## 9 Biggs … 183 84 black light brown 24 male mascu…
## 10 Obi-Wa… 182 77 auburn, wh… fair blue-gray 57 male mascu…
## # … with 77 more rows, and 5 more variables: homeworld <chr>, species <chr>,
## # films <list>, vehicles <list>, starships <list>- Tamaño muestral: comunmente denotado como \(n\), es el número de individuos seleccionados de nuestra población (normalmente el número de filas de nuestros conjuntos de datos).
# Tamaño muestral
nrow(starwars)## [1] 8723.1.2 Incursión en lo aleatorio
Un experimento aleatorio es aquel cuyo resultado inmediato, para cada individuo, no es posible saber con certeza, aunque eso no impida definir y conocer su patrón a nivel poblacional (teórico). No sabemos que saldrá en el dado en cada tirada pero sí la probabilidad de cada dígito, pudiendo incluso inferir resultados de nuestra población en función de nuestras muestras (tiradas): si de 1 millón de veces que tiramos el dado, en el 90% de ellas sale un 1, usando el conocimiento probabilístico de que la probabilidad de cada número debería ser de \(1/6\), podríamos inferir que nuestro dado podría estar trucado.
La forma más sencilla de generar una muestra aleatoria en R es con la función sample(), indicándole los siguientes argumentos:
x: los valores posibles (lo que se conoce como dominio). Por ejemplo, en el caso de una moneda, serán"cara"y"cruz".size: el número de veces que realizamos la extracción aleatoria (el número de tiradas).replace: en caso de estarTRUE, permitirá que puedan salir valores repetidos (por ejemplo,cara, cara). En caso de serFALSE, es como una urna de bolas de forma que tras cada extracción la bola nunca vuelve a la urna: solo se podrá realizar el experimento un máximo de veces igual al número de elementos enx
## [1] "cruz" "cruz" "cruz" "cruz" "cara" "cara" "cruz" "cruz" "cruz" "cara"
## [11] "cruz" "cara" "cara" "cruz" "cara" "cara" "cara" "cruz" "cruz" "cara"
## [21] "cruz" "cara" "cruz" "cara" "cruz" "cara" "cruz" "cara" "cara" "cruz"Si lo ejecutamos de nuevo, al ser aleatorio, saldrán otras 30 tiradas distintas.
sample(x = valores_moneda, size = 30, replace = TRUE)## [1] "cara" "cara" "cruz" "cara" "cara" "cruz" "cruz" "cara" "cara" "cruz"
## [11] "cara" "cruz" "cruz" "cruz" "cruz" "cruz" "cara" "cruz" "cruz" "cruz"
## [21] "cara" "cara" "cara" "cruz" "cara" "cara" "cara" "cara" "cruz" "cara"En el caso de la moneda es un experimento en el que los posibles sucesos son equiprobables: ambos tienen la mismas opciones de salir. Si tuviésemos el equivalente a una moneda trucada, donde por ejemplo "cara" tuviese un 0.7 de probabilidad y "cruz" un 0.3 (la suma debe ser siempre igual 1), obtendríamos tiradas muy diferentes. Para indicarle que las probabilidades asociadas al experimento no son iguales, usaremos el argumento probs, pasándole un vector con dichas probabilidades
tirada_equi <- sample(x = valores_moneda, size = 500, replace = TRUE)
tirada_trucada <- sample(x = valores_moneda, size = 500, prob = c(0.7, 0.3), replace = TRUE)
# Número de caras (de 500 tiradas)
sum(tirada_equi == "cara")## [1] 259
sum(tirada_trucada == "cara")## [1] 35223.1.3 Características y modalidades
En estadística llamamos caracteres a cada una de las variables o columnas de una tabla, cada una de las características o cualidades que se miden/estudian para cada uno de los individuos seleccionados en la muestra. En el caso de starwars, podemos extraer su nomnbre con names()
# Número de características medidas
ncol(starwars)## [1] 14
# Características
names(starwars)## [1] "name" "height" "mass" "hair_color" "skin_color"
## [6] "eye_color" "birth_year" "sex" "gender" "homeworld"
## [11] "species" "films" "vehicles" "starships"Y para cada una de ellas llamaremos modalidades a los diferentes valores que puede adoptar una característica o variable. En el caso por ejemplo del fichero de starwars tenemos distintas opciones:
-
sex: tiene 4 modalidadesfemale, hermaphroditic, male, none(podemos extraerlas conunique(), que nos dará los valores únicos de una variable).
unique(starwars$sex)## [1] "male" "none" "female" "hermaphroditic"
## [5] NA-
mass: su modalidad son todos los números reales positivos hasta un peso máximo (es lo que se conoce como una variable continua).
En estadística, como en probabilidad, podemos distinguir las variables en función de las modalidades permitidas en dos grandes categorías:
-
Variables categóricas (nominales o cualitativas). Son variables que representan categorías o cualidades. Ejemplos: color, forma, estado civil, religión, etc. Estas variables las podemos subdividir en función de si admiten o no un orden:
- Cualitativas ordinales: aunque representen cualidades, tienen una jerarquía de orden. Ejemplos: suspenso-aprobado-notable, sano - herido leve - grave, etc.
- Cualitativas nominales: no admiten (salvo problemas nuestros) una jerarquía de orden. Ejemplos: ateo-católico-musulmán, soltero-casado, homber-mujer, etc.
-
Variables cuantitativas: representan una cantidad numérica medible, una característica cuantificable matemáticamente. A su vez se pueden subdividir en dos grupos.
- Cuantitativas discretas: se pueden contar y enumerar (aunque sean infinitos), detrás de un valor puedo saber cuál viene después (personas, granos de arena, etc).
- Cuantitativas continuas: no solo toman infinitos valores sino que entre dos valores cualesquiera, también hay infinitos términos, no se puede determinar el siguiente valor a uno dado (estaturas, pesos, temperatura, etc).
23.2 Análisis univariante: cualitativas nominales
Como hemos comentado, vamos a empezar introduciendo algunas técnicas de análisis estadística para variables cualitativas o categóricas de manera univariante, variable a variable, analizando cada una de las columnas de un dataset de manera independiente del resto.
23.2.1 Factores
En el caso de las variables cualitativa, llamaremos niveles o modalidades a los diferentes valores que pueden tomar estos datos. Por ejemplo, en el caso de la variable sex del conjunto starwars, tenemos 4 niveles permitidos: female, hermaphroditic, male y none (amén de datos ausentes). Como ya hemos comentado en algunos apartados anteriores, este tipo de variables se conocen en R como factores en R. Y el paquete fundamental para tratarlos es forcats (del entorno tidyverse). Este paquete nos permite fijar los niveles (guardados internamente como levels) que toma una determinada variable categórica para que no puedan generarse equivocaciones, errores en la recolección y generación de datos. Además hace que su análisis sea menos costoso computacionalmente a la hora de hacer búsquedas y comparativas.
Veamos un ejempo sencillo definiendo una variable estado que tome los valores "sano", "leve" y "grave" de la siguiente manera.
estado <-
c("grave", "leve", "sano", "sano", "sano", "grave",
"grave", "leve", "grave", "sano", "sano")
estado## [1] "grave" "leve" "sano" "sano" "sano" "grave" "grave" "leve" "grave"
## [10] "sano" "sano"La variable estado actualmente es de tipo texto, de tipo chr, algo que podemos comprobar con class(estado).
class(estado)## [1] "character"Desde un punto de vista estadístico y computacional, para R esta variable ahora mismo sería equivalente una variable de nombres. Pero estadísticamente no es lo mismo una variable con nombres (que identifican muchas veces el registro) que una variable categórica como estado que solo puede tomar esos 3 niveles.
¿Cómo convertir una variable a cualitativa o factor? Haciendo uso de la función as_factor del paquete forcats.
## [1] grave leve sano sano sano grave grave leve grave sano sano
## Levels: grave leve sano
class(estado_fct)## [1] "factor"No solo ha cambiado la clase de la variable sino que ahora, debajo del valor guardado, nos aparece la frase Levels: grave leve sano: son las modalidades o niveles de nuestra cualitativa. Imagina que ese día en el hospital no tuviésemos a nadie en estado grave: aunque ese día nuestra variable no tome dicho valor, el estado grave es un nivel permitido que podríamos tener, así que aunque lo eliminemos, por ser un factor, el nivel permanece (no lo tenemos ahora pero es un nivel permitido).-
estado_fct[estado_fct %in% c("sano", "leve")]## [1] leve sano sano sano leve sano sano
## Levels: grave leve sanoSi queremos indicarle que elimine un nivel no usado en ese momento podemos hacerlo con fct_drop()
fct_drop(estado_fct[estado_fct %in% c("sano", "leve")])## [1] leve sano sano sano leve sano sano
## Levels: leve sanoAl igual que podemos eliminar niveles podemos ampliar los niveles existentes (aunque no existan datos de ese nivel en ese momento) con fct_expand()
fct_expand(estado_fct, c("UCI", "fallecido"))## [1] grave leve sano sano sano grave grave leve grave sano sano
## Levels: grave leve sano UCI fallecidoAunque luego veremos como usar el count(), para variables de tipo factor podemos contar los elementos de cada nivel de una manera sencilla con fct_count()
fct_count(estado_fct)## # A tibble: 3 × 2
## f n
## <fct> <int>
## 1 grave 4
## 2 leve 2
## 3 sano 5Si te fijas el orden de los niveles es por orden de aparición en la variable, pero podemos ordenarlos por aparición con fct_infreq()
fct_infreq(estado_fct)## [1] grave leve sano sano sano grave grave leve grave sano sano
## Levels: sano grave leveA veces queremos agrupar niveles, por ejemplo, no permitiendo niveles que no sucedan un mínimo de veces. Con fct_lump_min(estado_fct, min = 4) le indicaremos que para que exista el nivel debe de suceder al menos 4 veces (las observaciones que no lo cumplan irán a un nivel genérico llamado Other, aunque se puede cambiar con el argumento other_level). Podemos hacer algo equivalente pero en función de su frecuencia relativa con fct_lump_prop().
fct_lump_min(estado_fct, min = 3)## [1] grave Other sano sano sano grave grave Other grave sano sano
## Levels: grave sano Other
fct_lump_min(estado_fct, min = 5)## [1] Other Other sano sano sano Other Other Other Other sano sano
## Levels: sano Other
fct_lump_min(estado_fct, min = 5, other_level = "otros")## [1] otros otros sano sano sano otros otros otros otros sano sano
## Levels: sano otrosComo ya hemos usado (y veremos en detalle un poco más adelante), con count() también podemos los valores de una variable asociados a cada modalidad. Por ejemplo, vamos a calcular la cantidad de personajes de cada especie (filtrando los ausentes).
## # A tibble: 37 × 2
## species n
## <chr> <int>
## 1 Aleena 1
## 2 Besalisk 1
## 3 Cerean 1
## 4 Chagrian 1
## 5 Clawdite 1
## 6 Droid 6
## 7 Dug 1
## 8 Ewok 1
## 9 Geonosian 1
## 10 Gungan 3
## # … with 27 more rowsAhora que sabemos hacerlo podemos dibujar un diagrama de barras para visualizar el número de personajes de cada especie (con fill = n y scale_fill_continuous_tableau() asignaremos un gradiente de color en función de la frecuencia).
ggplot(starwars %>%
filter(!is.na(species)) %>%
count(species),
aes(y = species, x = n, fill = n)) +
geom_col() +
scale_fill_continuous_tableau() +
labs(fill = "Frecuencia absoluta",
x = "Número de personajes", y = "Especies")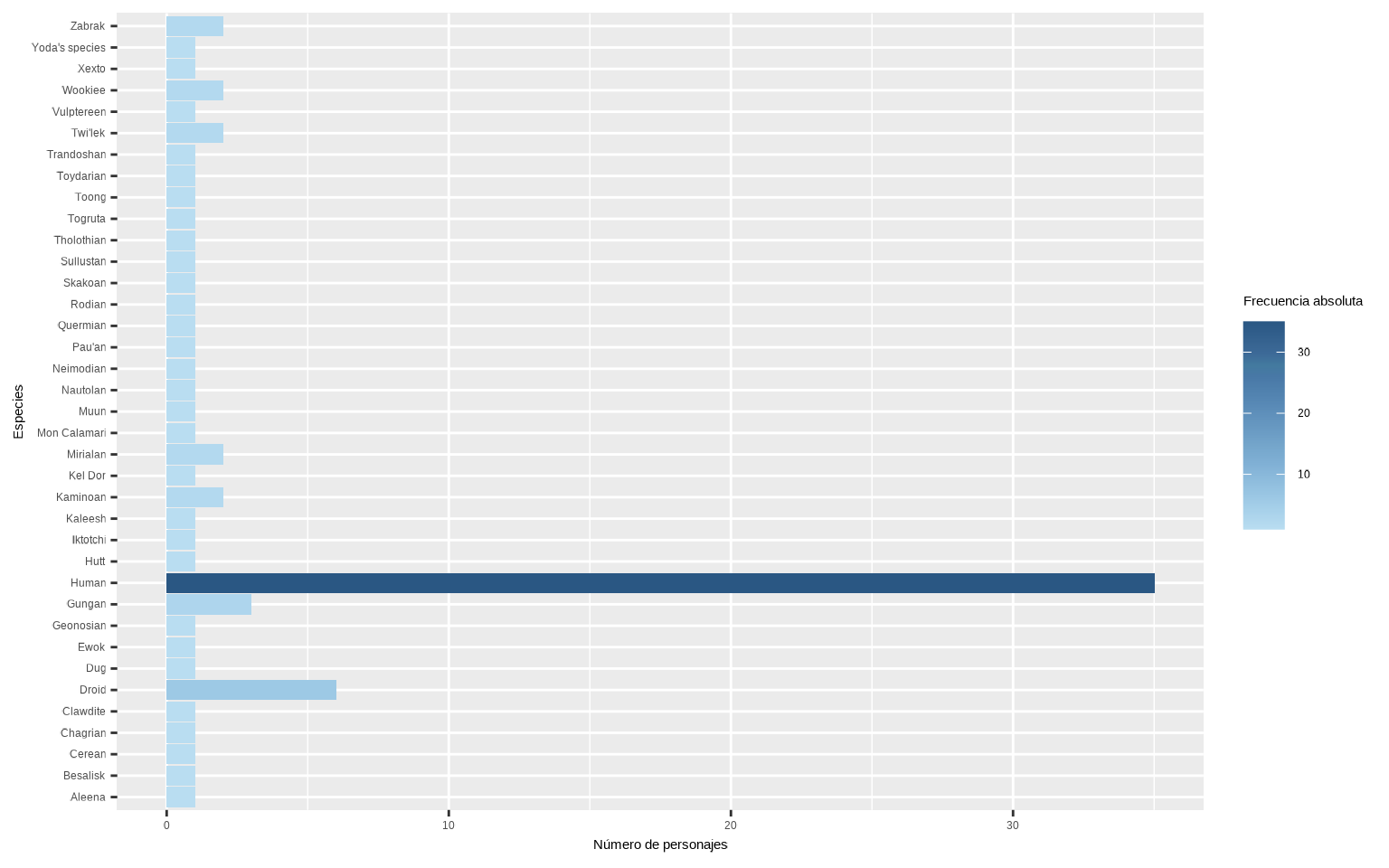
Al tener muchos niveles de species con muy pocos elementos, tenemos un gráfico poco claro, así que vamos a indicarle que nos convierta species a factor, y que nos agrupe aquellas niveles que tengan menos de 2 personajes.
ggplot(starwars %>%
filter(!is.na(species)) %>%
mutate(species =
fct_lump_min(species, min = 3,
other_level = "Otras especies")) %>%
count(species),
aes(y = species, x = n, fill = n)) +
geom_col() +
scale_fill_continuous_tableau() +
labs(fill = "Frecuencia absoluta",
x = "Número de personajes", y = "Especies")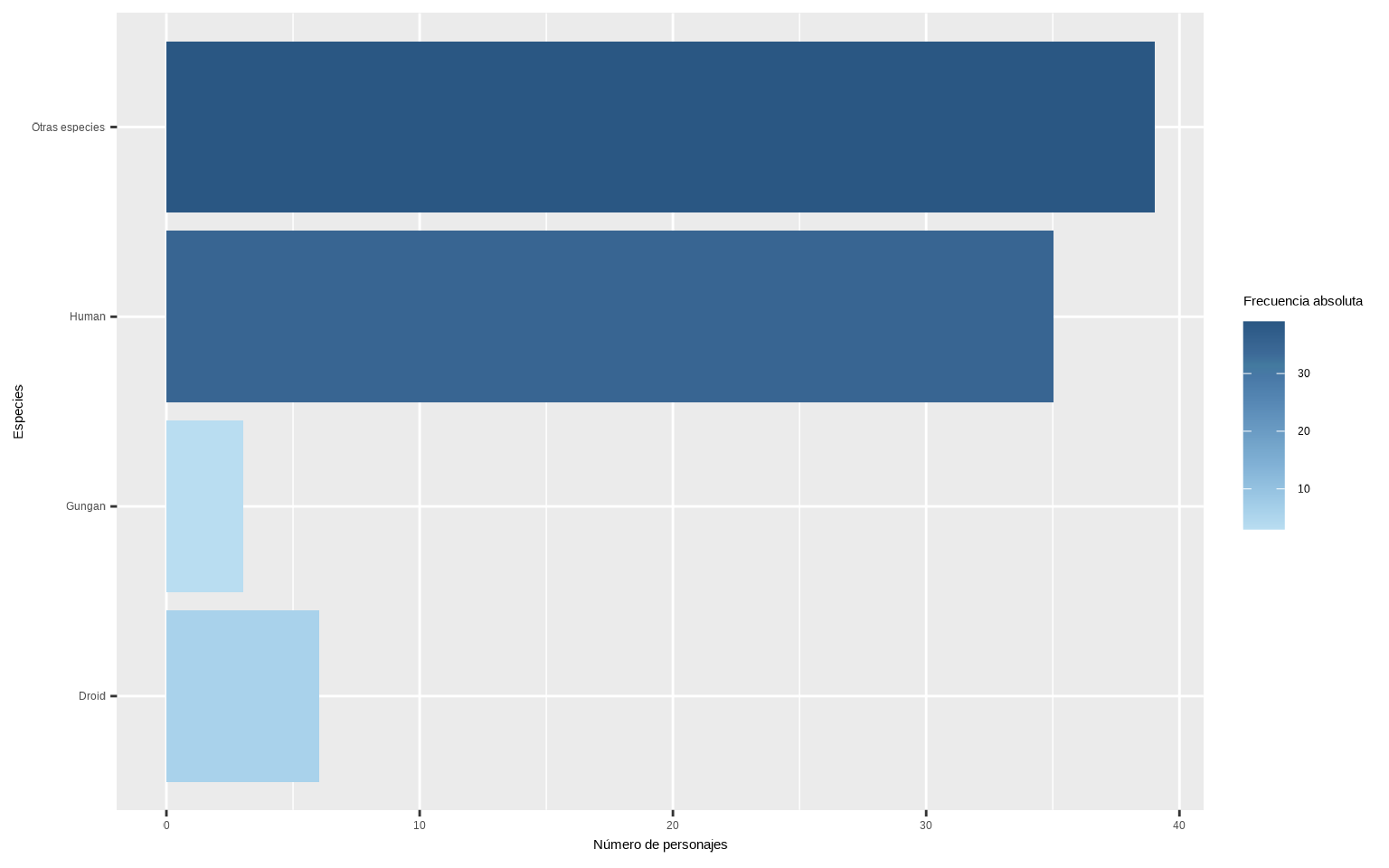
Por último vamos a aplicar algunos ajustes del tema que ya hemos visto en apartados anteriores para terminar nuestro gráfico.
library(showtext)
font_add_google(family = "Roboto", name = "Roboto")
showtext_auto()
ggplot(starwars %>%
filter(!is.na(species)) %>%
mutate(species =
fct_lump_min(species, min = 3,
other_level = "Otras especies")) %>%
count(species),
aes(y = species, x = n, fill = n)) +
geom_col() +
scale_fill_continuous_tableau() +
labs(fill = "Frecuencia absoluta",
x = "Número de personajes", y = "Especies") +
theme(panel.background = element_rect(fill = "white"),
plot.background = element_rect(fill = "white",
color = "white"),
panel.grid.major.y =
element_line(size = 0.05, color = "black"),
panel.grid.major.x =
element_line(size = 0.1, color = "black"),
text = element_text(size = 13),
axis.title =
element_text(family = "Roboto", size = 23),
axis.text.x = element_text(family = "Roboto",
size = 15),
axis.text.y = element_text(family = "Roboto",
size = 15))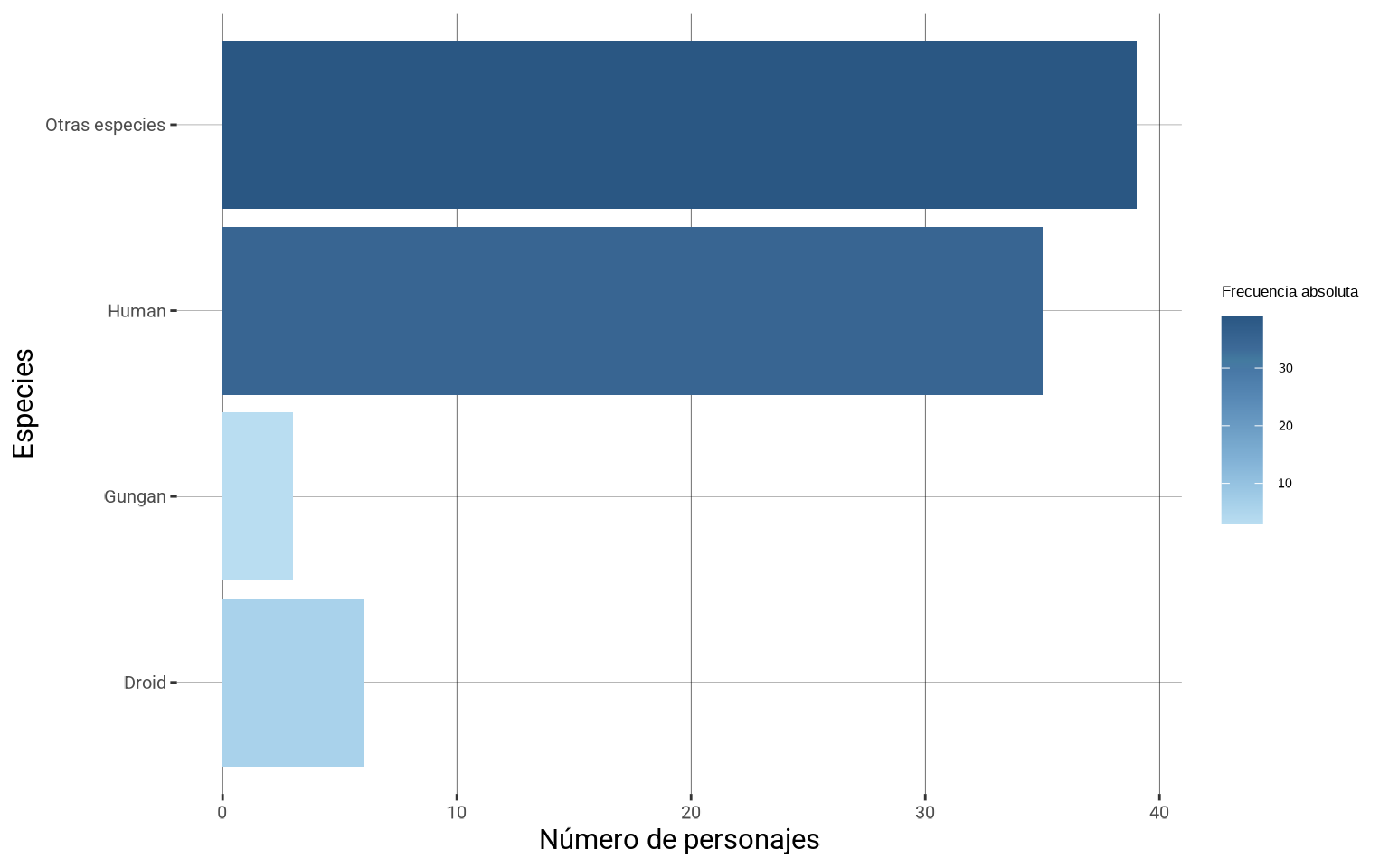
23.2.2 Tablas de frecuencias
Una de las primeras cosas que uno aprende en la asignatura de estadística descriptiva es saber resumir nuestros datos cuando tenemos muchos, y además muchos valores repetidos. Vamos a construir la tabla de frecuencias de la variable n_films de nuestro ya conocido conjunto starwars (una variable que vamos a crear contando en cuántas películas aparece cada personaje con map_int() para aplicar la función length() a cada lista de cada personaje guardada en films)
library(purrr)
library(tidyverse)
starwars_nueva <- starwars %>%
mutate(n_films = map_int(films, length))Y lo primero es contar: ¿cuántos registros hay de cada una de las clases? Para ello usaremos la función count()
starwars_nueva %>% count()## # A tibble: 1 × 1
## n
## <int>
## 1 87Como ves si aplicamos la función directamente simplemente nos cuenta el número de filas de la tabla, así que vamos a usar la misma función pero indicándole la variable creada.
tabla_freq <- starwars_nueva %>% count(n_films)
tabla_freq## # A tibble: 7 × 2
## n_films n
## <int> <int>
## 1 1 46
## 2 2 18
## 3 3 13
## 4 4 2
## 5 5 5
## 6 6 2
## 7 7 1Esa columna n es lo que conocemos como frecuencias absolutas, el número de veces que la variable toma dicha valor.
- Frecuencias absolutas: contar cuántos elementos aparecen de un determinado nivel. Suele ser denotada como \(n_i\), para cada nivel \(i\).
- Frecuencias relativas: contar que proporción del total representa dicha cantidad. Suele ser denotada como \(f_i\), para cada nivel \(i\).
Esa frecuencia absoluta también podemos calcularla haciendo uso de table(), aplicada a la variable extraída de la tabla.
table(starwars_nueva$n_films)##
## 1 2 3 4 5 6 7
## 46 18 13 2 5 2 1## [1] "table"El formato de la salida de table() es lo que se conoce como una tabla de contingencia. Aplicada a una sola variable es una tabla unidimensional con una fila compuesto por los niveles y una segunda con la frecuencia absoluta de cada uno de ellos. Si lo aplicamos a dos variables el resultado será una tabla de contigencia bidimensional: la primera variable en las filas, la segunda en las columnas, y realizará el conteo bidimensional \(n_ij\) para cada par de niveles \((i, j)\)
## n_films
## sex 1 2 3 4 5 6 7
## female 8 4 3 0 1 0 0
## hermaphroditic 0 0 1 0 0 0 0
## male 32 12 9 2 4 1 0
## none 3 1 0 0 0 1 1Una vez que tenemos las frecuencias absolutas, las relativas se pueden calcular de forma sencilla con prop.table(), que nos calcula la proporción que representa dicho valor.
# Construimos de cero
tabla_freq <- starwars_nueva %>%
# n: frecuencia absoluta
count(n_films) %>%
# f_i: frecuencia relativa
mutate(f_i = prop.table(n))
tabla_freq## # A tibble: 7 × 3
## n_films n f_i
## <int> <int> <dbl>
## 1 1 46 0.529
## 2 2 18 0.207
## 3 3 13 0.149
## 4 4 2 0.0230
## 5 5 5 0.0575
## 6 6 2 0.0230
## 7 7 1 0.0115Es importanten observar que prop.table() debe aplicarse sobre una tabla de contingencia. No nos da error al aplicarlo sobre un vector númerico, pero lo que nos dará no son la frecuencias relativas del vector numérico si no de un vector que tuviera esos números como frecuencias absolutas.
prop.table(starwars_nueva$n_films)## [1] 0.028901734 0.034682081 0.040462428 0.023121387 0.028901734 0.017341040
## [7] 0.017341040 0.005780347 0.005780347 0.034682081 0.017341040 0.011560694
## [13] 0.028901734 0.023121387 0.005780347 0.017341040 0.017341040 0.005780347
## [19] 0.028901734 0.028901734 0.017341040 0.005780347 0.005780347 0.011560694
## [25] 0.005780347 0.011560694 0.005780347 0.005780347 0.005780347 0.005780347
## [31] 0.005780347 0.017341040 0.005780347 0.011560694 0.005780347 0.005780347
## [37] 0.005780347 0.011560694 0.005780347 0.005780347 0.011560694 0.005780347
## [43] 0.005780347 0.017341040 0.005780347 0.005780347 0.005780347 0.017341040
## [49] 0.017341040 0.017341040 0.011560694 0.011560694 0.011560694 0.005780347
## [55] 0.017341040 0.011560694 0.005780347 0.005780347 0.005780347 0.011560694
## [61] 0.011560694 0.005780347 0.005780347 0.011560694 0.011560694 0.005780347
## [67] 0.005780347 0.005780347 0.005780347 0.005780347 0.005780347 0.005780347
## [73] 0.011560694 0.005780347 0.005780347 0.011560694 0.005780347 0.005780347
## [79] 0.011560694 0.011560694 0.005780347 0.005780347 0.005780347 0.005780347
## [85] 0.005780347 0.005780347 0.017341040También es posible calcular frecuencias absolutas bidimensionales por varias variables a la vez dentro de {tidvyerse} con el propio count(), pasándole dos variables diferentes.
starwars_nueva %>% count(sex, gender)## # A tibble: 6 × 3
## sex gender n
## <chr> <chr> <int>
## 1 female feminine 16
## 2 hermaphroditic masculine 1
## 3 male masculine 60
## 4 none feminine 1
## 5 none masculine 5
## 6 <NA> <NA> 4Podemos también añadir una columna \(N_i\) de frecuencia absoluta acumulada, una columna que nos diga el número de personajes que han hecho un número de películas igual o menor que el indicado (usando la función cumsum() que nos realiza esa suma acumulada).
# Construimos de cero
tabla_freq <-
starwars_nueva %>%
# n: frecuencia absoluta
count(n_films) %>%
mutate(f_i = prop.table(n),
N_i = cumsum(n)) # cumsum calcula la suma acumulada
tabla_freq## # A tibble: 7 × 4
## n_films n f_i N_i
## <int> <int> <dbl> <int>
## 1 1 46 0.529 46
## 2 2 18 0.207 64
## 3 3 13 0.149 77
## 4 4 2 0.0230 79
## 5 5 5 0.0575 84
## 6 6 2 0.0230 86
## 7 7 1 0.0115 87Y al igual que sucedía con \(n_i\), la frecuencia absoluta acumulada \(N_i\) podremos también convertirla a frecuencia relativa acumulada.
# Construimos de cero
tabla_freq <- starwars_nueva %>%
count(n_films) %>%
mutate(N_i = cumsum(n)) %>% # cumsum calcula la suma acumulada
mutate(f_i = prop.table(n), # prop.table nos devuelve proporciones
F_i = cumsum(f_i))
tabla_freq## # A tibble: 7 × 5
## n_films n N_i f_i F_i
## <int> <int> <int> <dbl> <dbl>
## 1 1 46 46 0.529 0.529
## 2 2 18 64 0.207 0.736
## 3 3 13 77 0.149 0.885
## 4 4 2 79 0.0230 0.908
## 5 5 5 84 0.0575 0.966
## 6 6 2 86 0.0230 0.989
## 7 7 1 87 0.0115 1
# otra forma
tabla_freq <- starwars_nueva %>%
count(n_films) %>%
mutate(N_i = cumsum(n)) %>%
mutate(f_i = prop.table(n),
F_i = prop.table(N_i))
tabla_freq## # A tibble: 7 × 5
## n_films n N_i f_i F_i
## <int> <int> <int> <dbl> <dbl>
## 1 1 46 46 0.529 0.0880
## 2 2 18 64 0.207 0.122
## 3 3 13 77 0.149 0.147
## 4 4 2 79 0.0230 0.151
## 5 5 5 84 0.0575 0.161
## 6 6 2 86 0.0230 0.164
## 7 7 1 87 0.0115 0.166Esas frecuencias relativas quizás querramos tenerlas expresadas en porcentajes en lugar de en proporciones, lo que podemos fácilmente multiplicando esas proporciones por 100.
# Pasamos frecuencias relativas a porcentajes
tabla_freq %>% mutate(f_i = f_i * 100,
F_i = F_i * 100)## # A tibble: 7 × 5
## n_films n N_i f_i F_i
## <int> <int> <int> <dbl> <dbl>
## 1 1 46 46 52.9 8.80
## 2 2 18 64 20.7 12.2
## 3 3 13 77 14.9 14.7
## 4 4 2 79 2.30 15.1
## 5 5 5 84 5.75 16.1
## 6 6 2 86 2.30 16.4
## 7 7 1 87 1.15 16.6Por último, con la tabla tabla_freq expresando las frecuencias relativas en proporciones, vamos a cambiar el nombre de las columnas para que tengan los típicos nombres de una tabla de frecuencias.
# Renombramos
tabla_freq <- tabla_freq %>%
rename(n_i = n, x_i = n_films)
tabla_freq## # A tibble: 7 × 5
## x_i n_i N_i f_i F_i
## <int> <int> <int> <dbl> <dbl>
## 1 1 46 46 0.529 0.0880
## 2 2 18 64 0.207 0.122
## 3 3 13 77 0.149 0.147
## 4 4 2 79 0.0230 0.151
## 5 5 5 84 0.0575 0.161
## 6 6 2 86 0.0230 0.164
## 7 7 1 87 0.0115 0.166Con el paquete DT se pueden visualizar tablas en documentos .Rmd
¿Cuál es el color de pelo que más aparece en starwars?
Vamos a construir su tabla de frecuencias, primero conviertiendo hair_color a factor y viendo los niveles de dicha variable, y quedándonos solo con la variables name y hair_color. Además los niveles ausentes los vamos a convertir a "none", nivel que ya existe, con fct_explicit_na()
starwars_hair <-
starwars %>%
mutate(hair_color = fct_explicit_na(hair_color, na_level = "none")) %>%
select(c(name, hair_color))
starwars_hair## # A tibble: 87 × 2
## name hair_color
## <chr> <fct>
## 1 Luke Skywalker blond
## 2 C-3PO none
## 3 R2-D2 none
## 4 Darth Vader none
## 5 Leia Organa brown
## 6 Owen Lars brown, grey
## 7 Beru Whitesun lars brown
## 8 R5-D4 none
## 9 Biggs Darklighter black
## 10 Obi-Wan Kenobi auburn, white
## # … with 77 more rowsTras el preprocesamiento construimos nuestra tabla de frecuencias.
tabla_freq <- starwars_hair %>%
count(hair_color) %>%
mutate(N_i = cumsum(n)) %>% # cumsum calcula la suma acumulada
mutate(f_i = prop.table(n), # prop.table nos devuelve proporciones
F_i = cumsum(f_i))
tabla_freq## # A tibble: 12 × 5
## hair_color n N_i f_i F_i
## <fct> <int> <int> <dbl> <dbl>
## 1 auburn 1 1 0.0115 0.0115
## 2 auburn, grey 1 2 0.0115 0.0230
## 3 auburn, white 1 3 0.0115 0.0345
## 4 black 13 16 0.149 0.184
## 5 blond 3 19 0.0345 0.218
## 6 blonde 1 20 0.0115 0.230
## 7 brown 18 38 0.207 0.437
## 8 brown, grey 1 39 0.0115 0.448
## 9 grey 1 40 0.0115 0.460
## 10 none 42 82 0.483 0.943
## 11 unknown 1 83 0.0115 0.954
## 12 white 4 87 0.0460 1
# En porcentaje
tabla_freq <-
tabla_freq %>% mutate(f_i = 100 * f_i,
F_i = 100 * F_i)
tabla_freq ## # A tibble: 12 × 5
## hair_color n N_i f_i F_i
## <fct> <int> <int> <dbl> <dbl>
## 1 auburn 1 1 1.15 1.15
## 2 auburn, grey 1 2 1.15 2.30
## 3 auburn, white 1 3 1.15 3.45
## 4 black 13 16 14.9 18.4
## 5 blond 3 19 3.45 21.8
## 6 blonde 1 20 1.15 23.0
## 7 brown 18 38 20.7 43.7
## 8 brown, grey 1 39 1.15 44.8
## 9 grey 1 40 1.15 46.0
## 10 none 42 82 48.3 94.3
## 11 unknown 1 83 1.15 95.4
## 12 white 4 87 4.60 100En este caso las frecuencias acumuladas no nos aportan ningún significado ya que la variable que estamos resumiendo es cualitativa nominal, no hay un orden entre los colores (cómo si lo había entre el número de películas, que era una variable cuantitativa discreta).
23.2.3 Análisis gráfico
El principal diagrama para variables cualitativas (o cuantitativas discretas) es el diagrama de barras que ya hemos aprendido a generar y personalizar.
library(showtext)
font_add_google(family = "Roboto", name = "Roboto")
showtext_auto()
ggplot(starwars %>%
filter(!is.na(species)) %>%
mutate(species =
fct_lump_min(species, min = 3,
other_level = "Otras especies")) %>%
count(species),
aes(y = species, x = n, fill = n)) +
geom_col() +
scale_fill_continuous_tableau() +
labs(fill = "Frecuencia absoluta",
x = "Número de personajes", y = "Especies") +
theme(panel.background = element_rect(fill = "white"),
plot.background = element_rect(fill = "white",
color = "white"),
panel.grid.major.y =
element_line(size = 0.05, color = "black"),
panel.grid.major.x =
element_line(size = 0.1, color = "black"),
text = element_text(size = 13),
axis.title =
element_text(family = "Roboto", size = 23),
axis.text.x = element_text(family = "Roboto",
size = 15),
axis.text.y = element_text(family = "Roboto",
size = 15))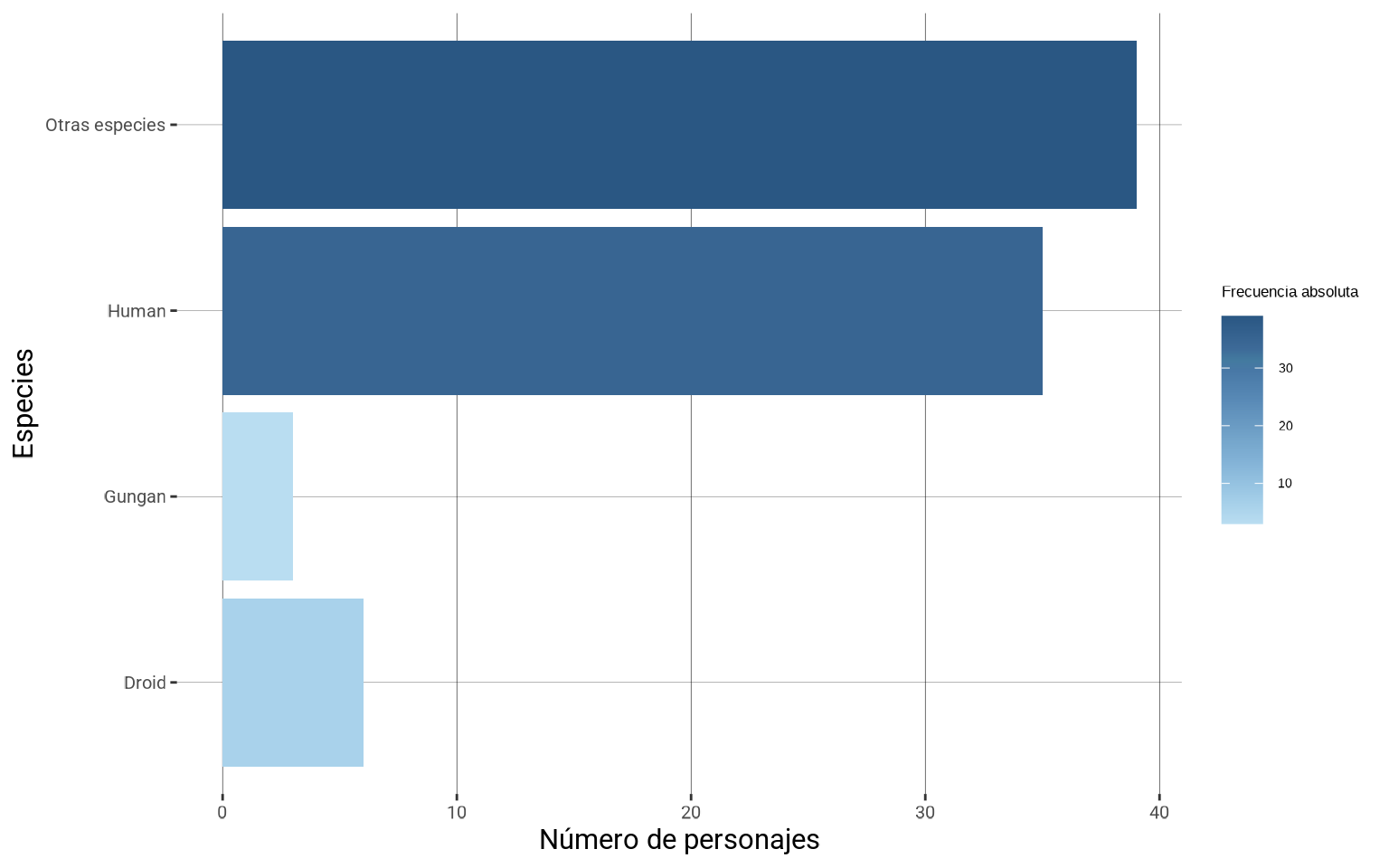
Otra opción con variables cualitativas, en especial para visualizar palabras en textos y documentos son precisamente las word cloud o nubes de palabras. Con el paquete wordcloud2 podrmeos visualizar las nubes de términos, por ejemplo de las especies de starwars (una vez filtrados los datos dusentes y reagrupado aquellas especies con solo un personaje). Con los parámetros size y color le indicaremos el tamaño base de las palabras y el patrón de colores elegir. Las palabras las visualizará en un tamaño relativo al número de veces que aparece.
# install.packages("wordcloud2)
library(wordcloud2)
wordcloud2(starwars %>% drop_na(species) %>%
mutate(species =
fct_lump_min(species, min = 2,
other_level = "otras")) %>%
count(species),
size = 0.8, color= 'random-dark')Otra opción habitual son los mosaicos o treemaps, representando en una cuadrícula cada una de las categorías, cuya área sea proprocional a las veces que aparece. Lo haremos con treemapify, dentro de la lógica ggplot2: los parámetros dentro de aes() serán
area (asociado a la frecuencia absoluta), fill (color del relleno) y label (nombre). Usaremos una de las paletas de colores de cuadros vistas, en este caso MetBrewer::met.brewer("Renoir").
# install.packages("treemapify")
library(treemapify)
ggplot(starwars %>% drop_na(species) %>%
mutate(species =
fct_lump_min(species, min = 2,
other_level = "otras")) %>%
count(species),
aes(area = n, fill = species, label = species)) +
geom_treemap() +
scale_fill_manual(values = MetBrewer::met.brewer("Renoir")) +
labs(fill = "Especies")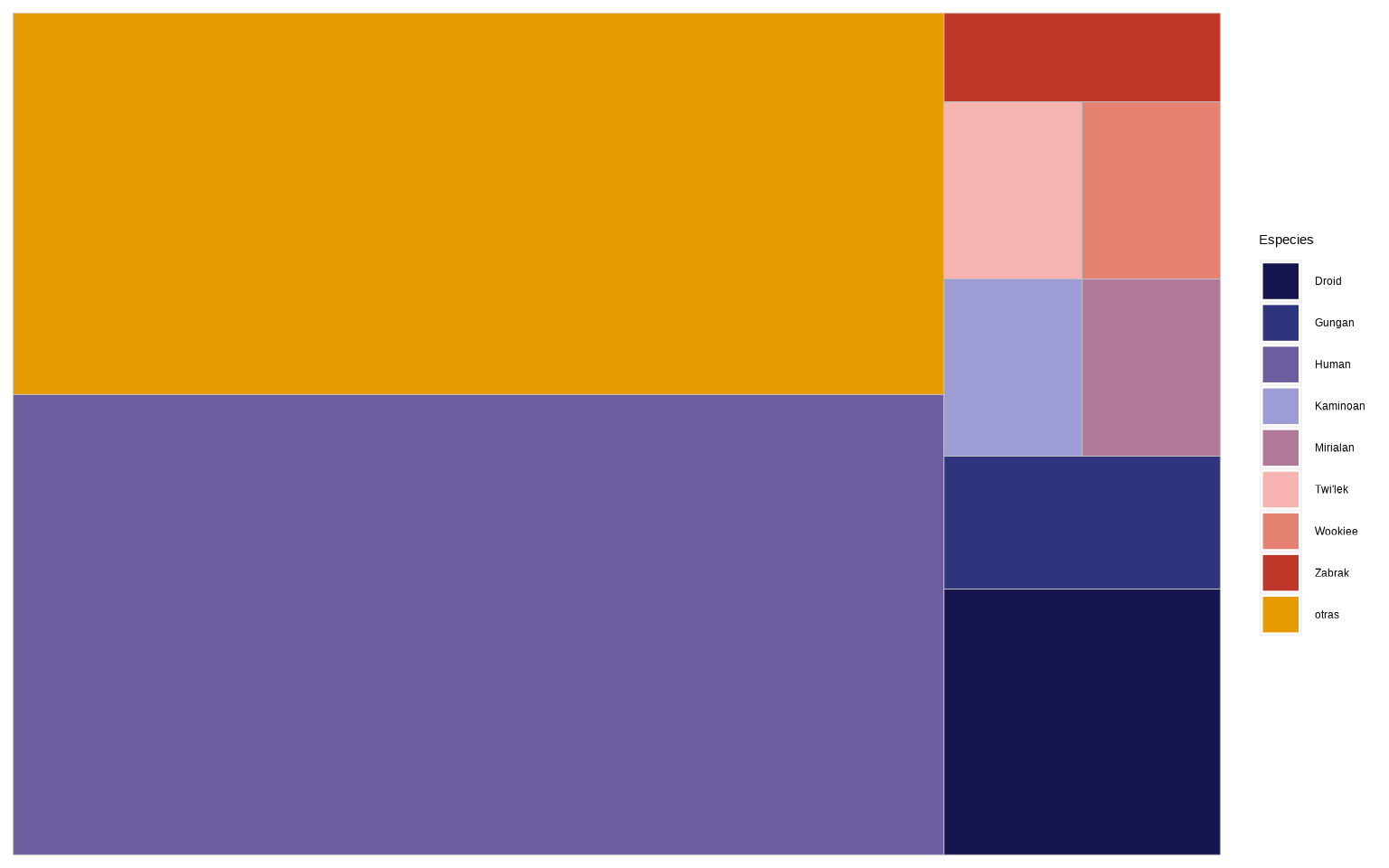
Con geom_treemap_text() podemos además escribir el nombre de los niveles, pudiendo eliminar la leyenda.
ggplot(starwars %>% drop_na(species) %>%
mutate(species =
fct_lump_min(species, min = 2,
other_level = "otras")) %>%
count(species),
aes(area = n, fill = species, label = species)) +
geom_treemap() +
geom_treemap_text(colour = "white", place = "centre",
size = 17) +
scale_fill_manual(values = MetBrewer::met.brewer("Renoir")) +
labs(fill = "Especies") +
guides(fill = "none")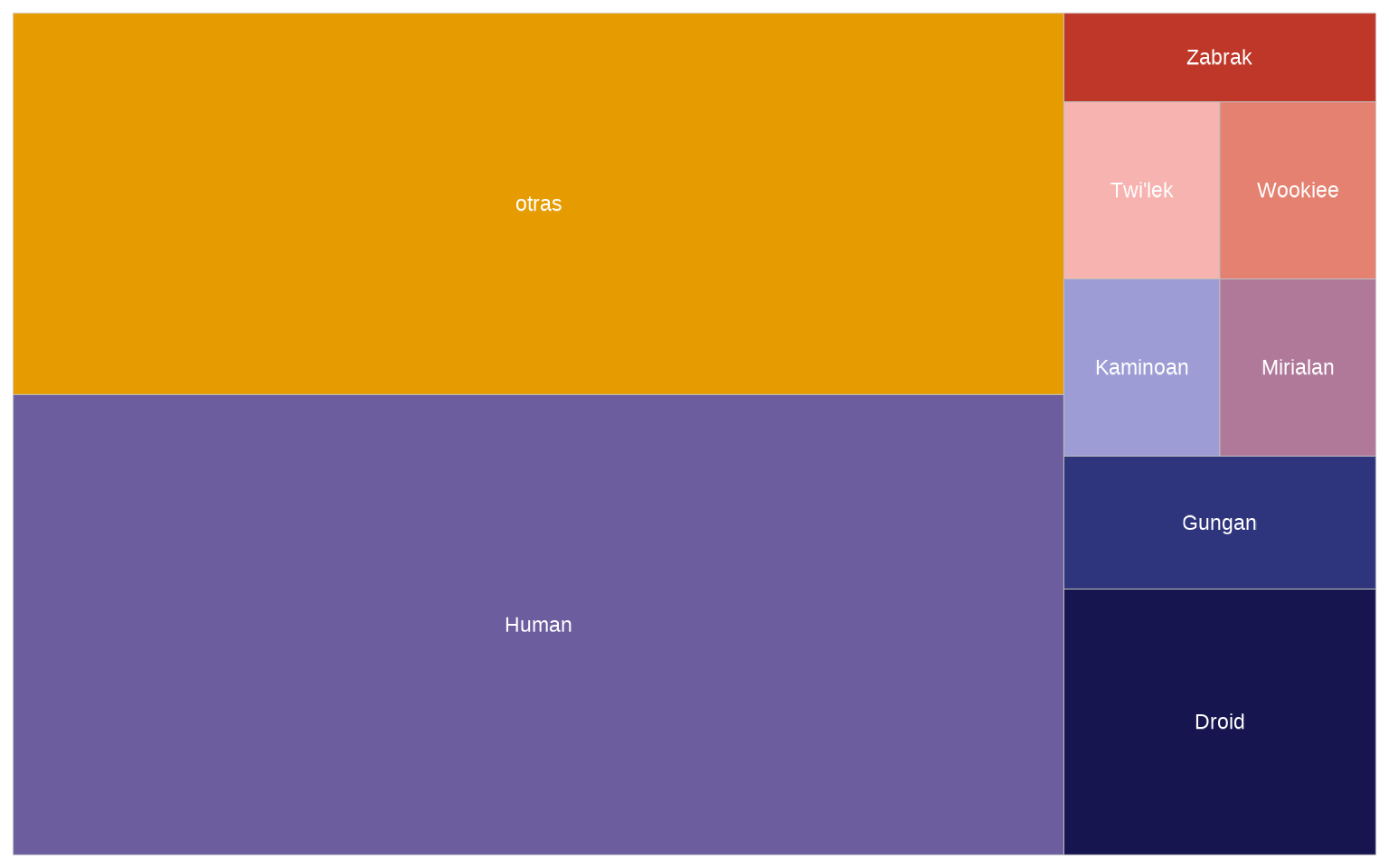
Por último vamos a probar el paquete ggparliament (puedes ver su documentación), para la representación de escaños (los partidos que se presentan a unas elecciones son variables cualitativas, y sus escaños sus frecuencias absolutas.
Para ilustrarlo vamos a usar el conjunto election_data de dicho paquete, que contiene los datos electorales de Rusia, Australia, Alemnia, UK y Estados Unidos
# install.packages("ggparliament")
library(ggparliament)
election_data## year country house party_long
## 1 2016 USA Senate Republican
## 2 2014 USA Senate Republican
## 3 2012 USA Senate Democratic
## 4 2016 USA Representatives Republican
## 5 2014 USA Representatives Republican
## 6 2012 USA Representatives Republican
## 7 2017 UK Commons Labour
## 8 2017 UK Commons Scottish National Party
## 9 2017 UK Commons Liberal Democrats
## 10 2017 UK Commons Democratic Unionist
## 11 2017 UK Commons Sinn Fein
## 12 2017 UK Commons Plaid Cymru
## 13 2017 UK Commons Green
## 14 2017 UK Commons Independent
## 15 2015 UK Commons Labour
## 16 2015 UK Commons Scottish National Party
## 17 2015 UK Commons Liberal Democrats
## 18 2015 UK Commons Democratic Unionist
## 19 2015 UK Commons Sinn Fein
## 20 2015 UK Commons Plaid Cymru
## 21 2015 UK Commons Social Democratic & Labour
## 22 2015 UK Commons Ulster Unionist
## 23 2015 UK Commons UK Independence Party
## 24 2015 UK Commons Green
## 25 2015 UK Commons Independent
## 26 2010 UK Commons Labour
## 27 2010 UK Commons Democratic Unionist
## 28 2010 UK Commons Scottish National Party
## 29 2010 UK Commons Sinn Fein
## 30 2010 UK Commons Plaid Cymru
## 31 2010 UK Commons Social Democratic & Labour
## 32 2010 UK Commons Green
## 33 2010 UK Commons Alliance
## 34 2010 UK Commons Independent
## 35 2016 Australia Representatives Labour
## 36 2016 Australia Representatives Greens
## 37 2016 Australia Representatives Xenophon Team
## 38 2016 Australia Representatives Independent
## 39 2016 Australia Representatives Katter's Australian
## 40 2013 Australia Representatives Labour
## 41 2013 Australia Representatives Independent
## 42 2013 Australia Representatives Greens
## 43 2013 Australia Representatives Palmer United
## 44 2013 Australia Representatives Katter's Australian
## 45 2010 Australia Representatives Liberal
## 46 2010 Australia Representatives Liberal National
## 47 2010 Australia Representatives National
## 48 2010 Australia Representatives Greens
## 49 2010 Australia Representatives Nationals WA
## 50 2010 Australia Representatives Country Liberal
## 51 2016 Australia Senate Labour
## 52 2016 Australia Senate Greens
## 53 2016 Australia Senate Hanson's One Nation
## 54 2016 Australia Senate Xenophon Team
## 55 2016 Australia Senate Liberal Democrats
## 56 2016 Australia Senate Family First
## 57 2016 Australia Senate Lambie Network
## 58 2016 Australia Senate Hinch's Justice Party
## 59 2013 Australia Senate Labour
## 60 2013 Australia Senate Greens
## 61 2013 Australia Senate Palmer United
## 62 2013 Australia Senate Xenophon Team
## 63 2013 Australia Senate Liberal Democrats
## 64 2013 Australia Senate Family First
## 65 2013 Australia Senate Democratic Labour
## 66 2013 Australia Senate Motoring Enthusiast
## 67 2010 Australia Senate Labour
## 68 2010 Australia Senate Greens
## 69 2010 Australia Senate Democratic Labour
## 70 2010 Australia Senate Independent
## 71 2016 Russia Duma Communist
## 72 2016 Russia Duma Liberal Democratic Party of Russia
## 73 2016 Russia Duma A Just Russia
## 74 2016 Russia Duma Rodina
## 75 2016 Russia Duma Civic Platform
## 76 2016 Russia Duma Independent
## 77 2011 Russia Duma Communist
## 78 2011 Russia Duma A Just Russia
## 79 2011 Russia Duma Liberal Democratic Party of Russia
## 80 2007 Russia Duma Communist
## 81 2007 Russia Duma Liberal Democratic Party of Russia
## 82 2007 Russia Duma A Just Russia
## 83 2016 USA Senate Democratic
## 84 2016 USA Senate Independent
## 85 2014 USA Senate Democratic
## 86 2014 USA Senate Independent
## 87 2012 USA Senate Republican
## 88 2012 USA Senate Independent
## 89 2016 USA Representatives Democratic
## 90 2014 USA Representatives Democratic
## 91 2012 USA Representatives Democratic
## 92 2005 Germany Bundestag Social Democratic Party
## 93 2017 Germany Bundestag Social Democratic Party
## 94 2009 Germany Bundestag Free Democratic Party
## 95 1990 Germany Bundestag Free Democratic Party
## 96 2009 Germany Bundestag The Left
## 97 2017 Germany Bundestag The Left
## 98 2009 Germany Bundestag Alliance 90/The Greens
## 99 2017 Germany Bundestag Alliance 90/The Greens
## 100 2013 Germany Bundestag The Left
## 101 2013 Germany Bundestag Alliance 90/The Greens
## 102 2005 Germany Bundestag Free Democratic Party
## 103 2002 Germany Bundestag Christian Social Union in Bavaria
## 104 2013 Germany Bundestag Christian Social Union in Bavaria
## 105 2002 Germany Bundestag Alliance 90/The Greens
## 106 2005 Germany Bundestag The Left
## 107 2005 Germany Bundestag Alliance 90/The Greens
## 108 1990 Germany Bundestag Christian Social Union in Bavaria
## 109 1994 Germany Bundestag Christian Social Union in Bavaria
## 110 1994 Germany Bundestag Alliance 90/The Greens
## 111 2002 Germany Bundestag Free Democratic Party
## 112 1998 Germany Bundestag Christian Social Union in Bavaria
## 113 1998 Germany Bundestag Alliance 90/The Greens
## 114 1994 Germany Bundestag Free Democratic Party
## 115 2017 Germany Bundestag Christian Social Union in Bavaria
## 116 2005 Germany Bundestag Christian Social Union in Bavaria
## 117 1998 Germany Bundestag Free Democratic Party
## 118 1998 Germany Bundestag Party of Democratic Socialism
## 119 1994 Germany Bundestag Party of Democratic Socialism
## 120 1990 Germany Bundestag Party of Democratic Socialism
## 121 1990 Germany Bundestag Alliance 90/The Greens
## 122 2002 Germany Bundestag Party of Democratic Socialism
## 123 2017 UK Commons Conservative
## 124 2015 UK Commons Conservative
## 125 2010 UK Commons Conservative
## 126 2010 UK Commons Liberal Democrats
## 127 2016 Australia Representatives Liberal
## 128 2016 Australia Representatives Liberal National
## 129 2016 Australia Representatives National
## 130 2013 Australia Representatives Liberal
## 131 2013 Australia Representatives Liberal National
## 132 2013 Australia Representatives National
## 133 2013 Australia Representatives Country Liberal
## 134 2010 Australia Representatives Independent
## 135 2010 Australia Representatives Labour
## 136 2016 Australia Senate Liberal
## 137 2016 Australia Senate Liberal National
## 138 2016 Australia Senate National
## 139 2016 Australia Senate Country Liberal
## 140 2013 Australia Senate Liberal
## 141 2010 Australia Senate Liberal
## 142 2010 Australia Senate Liberal National
## 143 2010 Australia Senate National
## 144 2010 Australia Senate Country Liberal
## 145 2016 Russia Duma United Russia
## 146 2011 Russia Duma United Russia
## 147 2007 Russia Duma United Russia
## 148 1998 Germany Bundestag Social Democratic Party
## 149 1990 Germany Bundestag Christian Democratic Union
## 150 2013 Germany Bundestag Christian Democratic Union
## 151 1994 Germany Bundestag Social Democratic Party
## 152 2002 Germany Bundestag Social Democratic Party
## 153 1994 Germany Bundestag Christian Democratic Union
## 154 1990 Germany Bundestag Social Democratic Party
## 155 2005 Germany Bundestag Christian Democratic Union
## 156 2017 Germany Bundestag Christian Democratic Union
## 157 1998 Germany Bundestag Christian Democratic Union
## 158 2009 Germany Bundestag Christian Democratic Union
## 159 2013 Germany Bundestag Social Democratic Party
## 160 2002 Germany Bundestag Christian Democratic Union
## 161 2009 Germany Bundestag Social Democratic Party
## 162 2017 Germany Bundestag Alternative for Germany
## 163 2017 Germany Bundestag Free Democratic Party
## 164 2009 Germany Bundestag Christian Social Union in Bavaria
## party_short seats government colour
## 1 GOP 52 1 #E81B23
## 2 GOP 54 1 #E81B23
## 3 Dem 53 1 #3333FF
## 4 GOP 241 1 #E81B23
## 5 GOP 247 1 #E81B23
## 6 GOP 234 1 #E81B23
## 7 Lab 262 0 #DC241F
## 8 SNP 35 0 #FEF987
## 9 LibDem 12 0 #FAA61A
## 10 DUP 10 1 #D46A4C
## 11 SF 7 0 #008800
## 12 PC 4 0 #008142
## 13 Green 1 0 #6AB023
## 14 Ind 1 0 #B4B4B4
## 15 Lab 232 0 #DC241F
## 16 SNP 56 0 #FEF987
## 17 LibDem 8 0 #FAA61A
## 18 DUP 8 0 #D46A4C
## 19 SF 4 0 #008800
## 20 PC 3 0 #008142
## 21 SDLP 3 0 #99FF66
## 22 UUP 2 0 #9999FF
## 23 UKIP 1 0 #70147A
## 24 Green 1 0 #6AB023
## 25 Ind 1 0 #B4B4B4
## 26 Lab 258 0 #DC241F
## 27 DUP 8 0 #D46A4C
## 28 SNP 6 0 #FEF987
## 29 SF 5 0 #008800
## 30 PC 3 0 #008142
## 31 SDLP 3 0 #99FF66
## 32 Green 1 0 #6AB023
## 33 Alliance 1 0 #F6CB2F
## 34 Ind 1 0 #B4B4B4
## 35 Lab 69 0 #F00011
## 36 Green 1 0 #10C25B
## 37 Xenophon 1 0 #FF6300
## 38 Ind 2 0 #B8B8B8
## 39 Katter 1 0 #FE6F5E
## 40 Lab 55 0 #F00011
## 41 Ind 2 0 #B8B8B8
## 42 Green 1 0 #10C25B
## 43 Palmer 1 0 #FFED00
## 44 Katter 1 0 #FE6F5E
## 45 Lib 44 0 #080CAB
## 46 LNP 21 0 #1456F1
## 47 Nat 6 0 #008000
## 48 Green 1 0 #10C25B
## 49 Nat WA 1 0 #008000
## 50 CLP 1 0 #FF7F00
## 51 Lab 26 0 #F00011
## 52 Green 9 0 #10C25B
## 53 HON 4 0 #F8F16F
## 54 Xenophon 3 0 #FF6300
## 55 LibDem 1 0 #F9E518
## 56 FF 1 0 #00CCFF
## 57 Lambie 1 0 #FFFF00
## 58 Hinch 1 0 #002F5D
## 59 Lab 25 0 #F00011
## 60 Green 10 0 #10C25B
## 61 Palmer 3 0 #FFED00
## 62 Xenophon 1 0 #FF6300
## 63 LibDem 1 0 #F9E518
## 64 FF 1 0 #00CCFF
## 65 Dem Lab 1 0 #008080
## 66 Motoring 1 0 #191970
## 67 Lab 31 0 #F00011
## 68 Green 9 0 #10C25B
## 69 Dem Lab 1 0 #008080
## 70 Ind 1 0 #B4B4B4
## 71 CPRF 42 0 #D50000
## 72 LDPR 39 0 #2862B3
## 73 JR 23 0 #FAB512
## 74 Rodina 1 0 #EA484A
## 75 CPI 1 0 #641263
## 76 Ind 1 0 #B4B4B4
## 77 CPRF 92 0 #D50000
## 78 JR 64 0 #FAB512
## 79 LDPR 56 0 #2862B3
## 80 CPRF 57 0 #D50000
## 81 LDPR 40 0 #2862B3
## 82 JR 38 0 #FAB512
## 83 Dem 46 0 #3333FF
## 84 Ind 2 0 #B4B4B4
## 85 Dem 44 0 #3333FF
## 86 Ind 2 0 #B4B4B4
## 87 GOP 45 0 #E81B23
## 88 Ind 2 0 #B4B4B4
## 89 Dem 194 0 #3333FF
## 90 Dem 188 0 #3333FF
## 91 Dem 201 0 #3333FF
## 92 SDP 180 0 #EB001F
## 93 SDP 153 0 #EB001F
## 94 FDP 93 0 #FFED00
## 95 FDP 79 0 #FFED00
## 96 LINKE 76 0 #BE3075
## 97 LINKE 69 0 #BE3075
## 98 GRUNE 68 0 #64A12D
## 99 GRUNE 67 0 #64A12D
## 100 LINKE 64 0 #BE3075
## 101 GRUNE 63 0 #64A12D
## 102 FDP 61 0 #FFED00
## 103 CSU 58 0 #008AC5
## 104 CSU 56 0 #008AC5
## 105 GRUNE 55 0 #64A12D
## 106 LINKE 54 0 #BE3075
## 107 GRUNE 51 0 #64A12D
## 108 CSU 51 0 #008AC5
## 109 CSU 50 0 #008AC5
## 110 GRUNE 49 0 #64A12D
## 111 FDP 47 0 #FFED00
## 112 CSU 47 0 #008AC5
## 113 GRUNE 47 0 #64A12D
## 114 FDP 47 0 #FFED00
## 115 CSU 46 0 #008AC5
## 116 CSU 46 0 #008AC5
## 117 FDP 43 0 #FFED00
## 118 PDS 36 0 #CD1811
## 119 PDS 30 0 #CD1811
## 120 PDS 17 0 #CD1811
## 121 GRUNE 8 0 #64A12D
## 122 PDS 2 0 #CD1811
## 123 Con 317 1 #0087DC
## 124 Con 330 1 #0087DC
## 125 Con 306 1 #0087DC
## 126 LibDem 57 1 #FAA61A
## 127 Lib 45 1 #080CAB
## 128 LNP 21 1 #1456F1
## 129 Nat 10 1 #008000
## 130 Lib 58 1 #080CAB
## 131 LNP 22 1 #1456F1
## 132 Nat 9 1 #008000
## 133 CLP 1 1 #FF7F00
## 134 Ind 4 0 #B8B8B8
## 135 Lab 72 1 #F00011
## 136 Lib 21 1 #080CAB
## 137 LNP 5 1 #1456F1
## 138 Nat 3 1 #008000
## 139 CLP 1 1 #FF7F00
## 140 Lib 33 1 #080CAB
## 141 Lib 24 1 #080CAB
## 142 LNP 6 1 #1456F1
## 143 Nat 3 1 #008000
## 144 CLP 1 1 #FF7F00
## 145 UR 343 1 #0C2C84
## 146 UR 238 1 #0C2C84
## 147 UR 315 1 #0C2C84
## 148 SDP 298 1 #EB001F
## 149 CDU 268 1 #000000
## 150 CDU 255 1 #000000
## 151 SDP 252 1 #EB001F
## 152 SDP 251 1 #EB001F
## 153 CDU 244 1 #000000
## 154 SDP 239 1 #EB001F
## 155 CDU 222 1 #000000
## 156 CDU 200 1 #000000
## 157 CDU 198 1 #000000
## 158 CDU 194 1 #000000
## 159 SDP 193 1 #EB001F
## 160 CDU 190 1 #000000
## 161 SDP 146 1 #EB001F
## 162 AFD 94 1 #009EE0
## 163 FDP 80 1 #FFED00
## 164 CSU 45 1 #008AC5Vamos a filtrar solo los resultados de Rusia del 2016
rusia <- election_data %>%
filter(country == "Russia" & year == 2016)Con la función parliament_data construiremos los datos, preparados para ser visualizados en formato hemiciclo (con parl_rows le indicamos las fila del parlamento).
rusia_parlamento <-
as_tibble(parliament_data(election_data = rusia, type = "semicircle",
parl_rows = 9, party_seats = rusia$seats))
rusia_parlamento## # A tibble: 450 × 12
## year country house party_long party_short seats government colour x
## <int> <chr> <chr> <chr> <chr> <int> <int> <chr> <dbl>
## 1 2016 Russia Duma Communist CPRF 42 0 #D50000 -2
## 2 2016 Russia Duma Communist CPRF 42 0 #D50000 -1.88
## 3 2016 Russia Duma Communist CPRF 42 0 #D50000 -1.75
## 4 2016 Russia Duma Communist CPRF 42 0 #D50000 -1.62
## 5 2016 Russia Duma Communist CPRF 42 0 #D50000 -1.5
## 6 2016 Russia Duma Communist CPRF 42 0 #D50000 -1.38
## 7 2016 Russia Duma Communist CPRF 42 0 #D50000 -1.25
## 8 2016 Russia Duma Communist CPRF 42 0 #D50000 -1.12
## 9 2016 Russia Duma Communist CPRF 42 0 #D50000 -1
## 10 2016 Russia Duma Communist CPRF 42 0 #D50000 -2.00
## # … with 440 more rows, and 3 more variables: y <dbl>, row <int>, theta <dbl>Fíjate que por defecto ha incluido ya un color por partido (que podríamos cambiar en ggplot2. Tras ello, y dentro de la filosofía ggplot2, podremos representar los datos de nuestro parlamento.
parlamento <-
ggplot(rusia_parlamento,
aes(x = x, y = y, colour = party_short)) +
geom_parliament_seats()
parlamento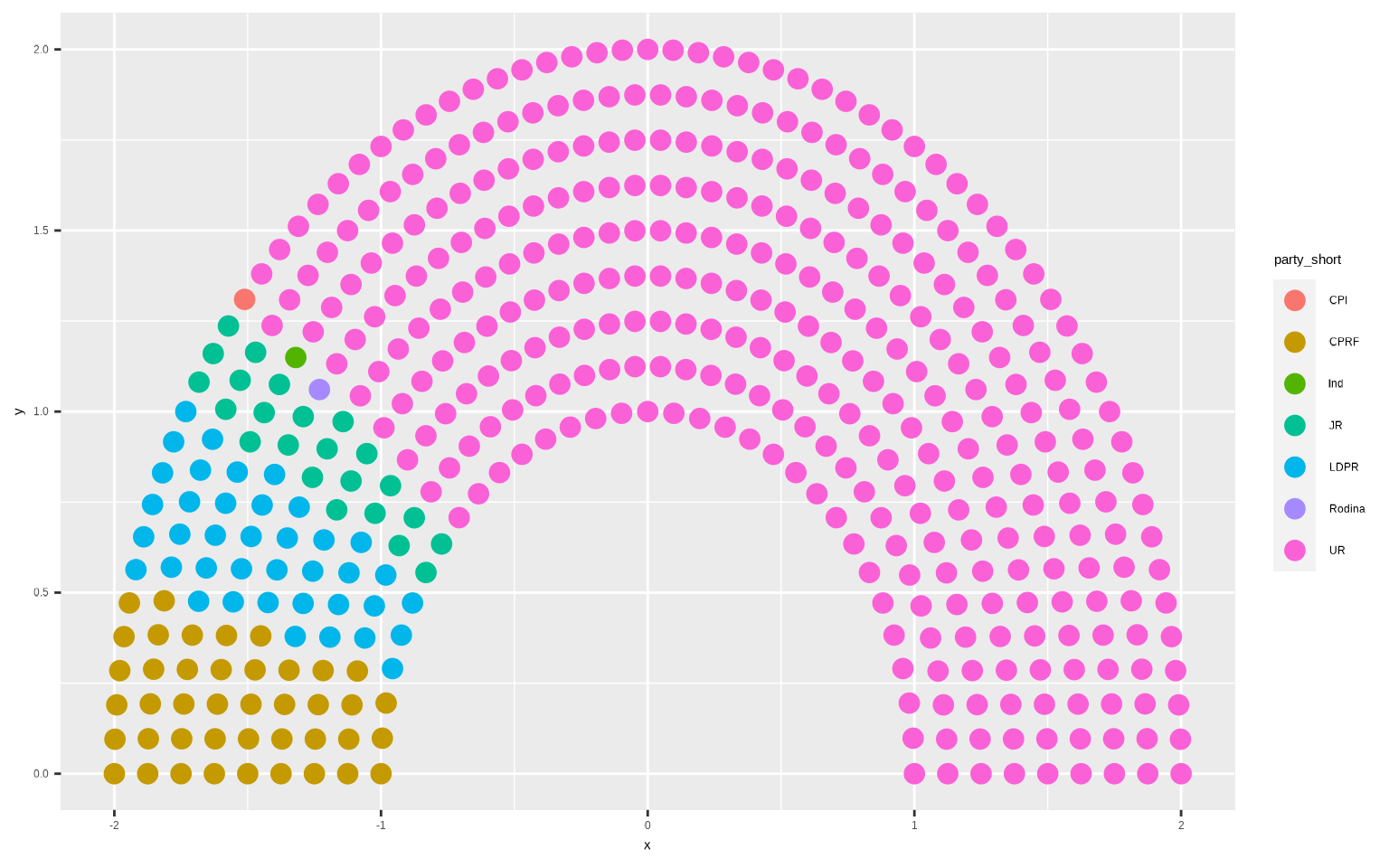
Podemos añadir las etiquetas de los partidos así como el número total de escaños
parlamento +
draw_partylabels(type = "semicircle",
party_names = party_long,
party_seats = seats,
party_colours = colour) +
draw_totalseats(n = 450, type = "semicircle")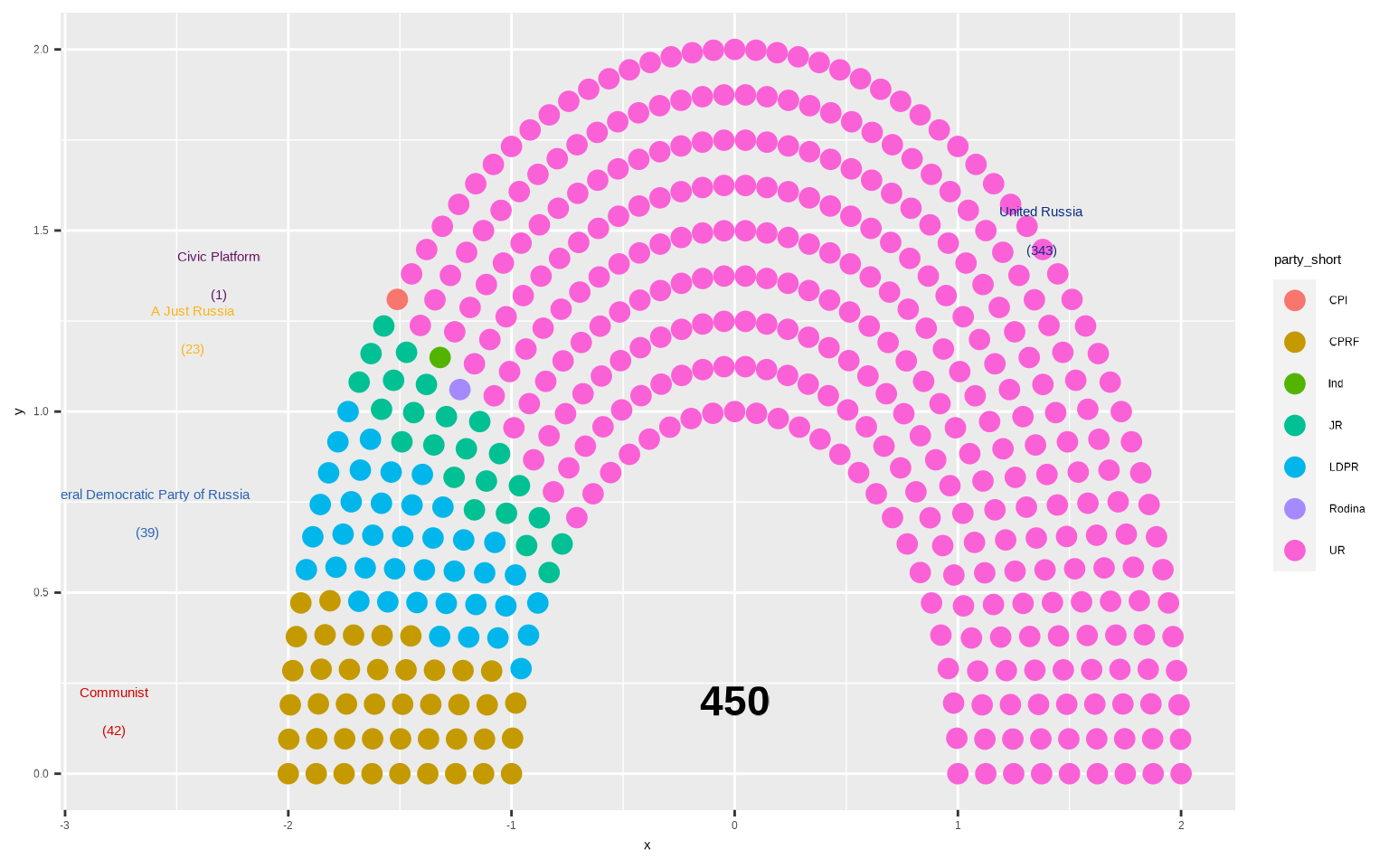
Con theme_ggparliament() tenemos un tema ya preparado para la representación del hemiciclo, y añadimos títulos y colores.
parlamento +
draw_totalseats(n = 450, type = "semicircle") +
theme_ggparliament() +
labs(color = "Partidos",
title = "Resultados de las elecciones de Rusia 2016") +
scale_colour_manual(values = rusia_parlamento$colour,
limits = rusia_parlamento$party_short) +
theme(plot.margin = margin(t = 4, r = 4, b = 4, l = 8, "pt"),
plot.title = element_text(size = 30))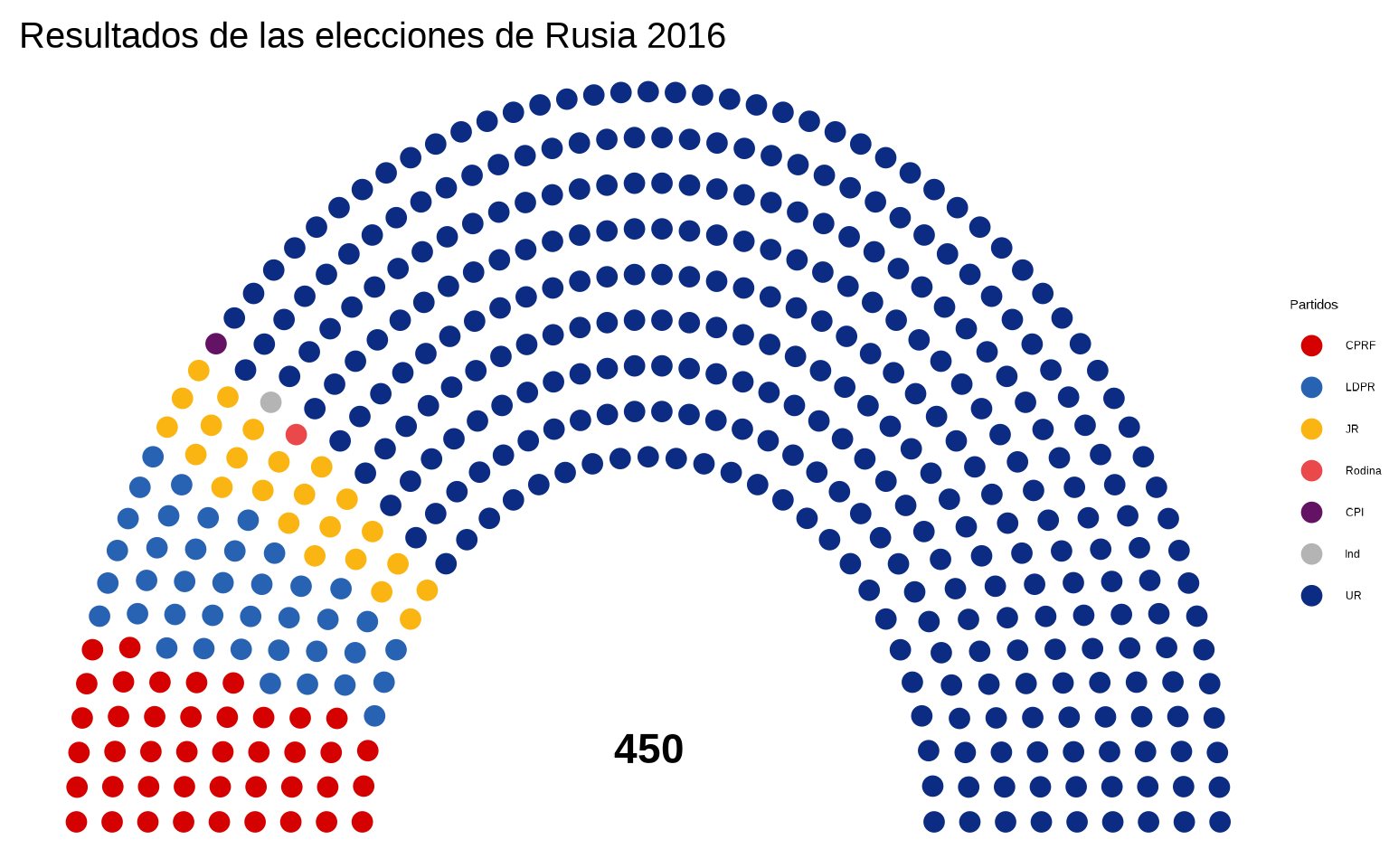
23.3 Análisis univariante: cualitativas ordinales
Ahora que sabemos describir datos cualitativos utilizando algunos conceptos fundamentales, vamos a profundizar en el análisis de un tipo de dato cuantitativo que son los datos ordinales.
Las variables ordinales son también cualidades no numéricas de objetos e individuos, pero en este caso tienen una jerarquía de orden que no solo permite ordenar sino acumular observaciones, es decir, estudiar cuantos elementos se acumulan por encima o por debajo de un nivel, qué variación hay de un nivel a otro, etc. Las variables ordinales no se caracterizan sólo por sus \(k\) niveles\(l_1,...l_k\), también se caracterizan por su relación de orden\(l_1 <...<l_k\)
Estos tipo de datos son muy frecuentes, por ejemplo, en estudios demográficos, en conceptos como nivel socioeconómico, nivel de estudios y en encuestas de opinión donde se suelen usar las escalas tipo Likert.
El concepto clave aquí es por lo tanto la frecuencia acumulada, que de nuevo podrá ser absoluta o relativa. La función cumsum() es la función fundamental para calcular estos valores sobre un conjunto de datos.
23.3.1 Tablas de frecuencias para ordinales
Vamos a construir la tabla de frecuencias acumuladas de la lista de notas del curso anterior, cuyos niveles son: "suspenso", "aprobado", "notable" y "sobresaliente". Su orden lo consideramos como: "suspenso" < "aprobado" < "notable" < "sobresaliente". Las calificaciones que han obtenido son las siguientes:
notas_curso <-
c("aprobado", "aprobado", "notable", "suspenso",
"suspenso", "aprobado", "notable", "sobresaliente",
"aprobado", "aprobado", "suspenso", "suspenso",
"suspenso", "aprobado", "sobresaliente", "notable",
"notable", "sobresaliente", "suspenso", "aprobado")
notas_curso## [1] "aprobado" "aprobado" "notable" "suspenso"
## [5] "suspenso" "aprobado" "notable" "sobresaliente"
## [9] "aprobado" "aprobado" "suspenso" "suspenso"
## [13] "suspenso" "aprobado" "sobresaliente" "notable"
## [17] "notable" "sobresaliente" "suspenso" "aprobado"Lo primero será ver cuántos registros hay de cada clase y con cuanta frecuencia aparecen. Para eso vamos a utilizar de nuevo la función count() tras pasar nuestros datos a formato tibble.
notas_curso <- tibble("notas" = notas_curso)
# Frecuencias absolutas + relativas
notas_freq <-
notas_curso %>%
count(notas) %>%
mutate(f = n / sum(n))
notas_freq## # A tibble: 4 × 3
## notas n f
## <chr> <int> <dbl>
## 1 aprobado 7 0.35
## 2 notable 4 0.2
## 3 sobresaliente 3 0.15
## 4 suspenso 6 0.3Observamos que tenemos las siguientes calificaciones: 6 suspensos, 7 aprobados, 4 notables y 3 sobresalientes. Sin embargo, esto no responde a la pregunta de cuántos de los alumnos han obtenido una calificación inferior a notable. Para ello vamos a calcular la tabla de frecuencias acumuladas:
- \(n_i\): frecuencia absoluta
- \(N_i\): absoluta acumulada
- \(f_i\): relativa
- \(F_i\): acumulada.
Para ello antes vamos a convertir la variable a factor, indicándole que es ordinal, con los niveles ordeandos y ordered = TRUE
notas_curso <- notas_curso %>%
mutate(notas =
factor(notas,
levels = c("suspenso", "aprobado",
"notable", "sobresaliente"),
ordered = TRUE))
notas_curso %>% pull(notas)## [1] aprobado aprobado notable suspenso suspenso
## [6] aprobado notable sobresaliente aprobado aprobado
## [11] suspenso suspenso suspenso aprobado sobresaliente
## [16] notable notable sobresaliente suspenso aprobado
## Levels: suspenso < aprobado < notable < sobresaliente
notas_freq_acum <-
notas_curso %>%
count(notas) %>%
rename(n_i = n) %>%
mutate(f_i = n_i / sum(n_i),
N_i = cumsum(n_i),
F_i = cumsum(N_i))
notas_freq_acum## # A tibble: 4 × 5
## notas n_i f_i N_i F_i
## <ord> <int> <dbl> <int> <int>
## 1 suspenso 6 0.3 6 6
## 2 aprobado 7 0.35 13 19
## 3 notable 4 0.2 17 36
## 4 sobresaliente 3 0.15 20 56Podemos visualizar tanto las acmuladas como las no acumuladas con un diagrama de barras.
library(MetBrewer)
ggplot(notas_freq_acum,
aes(x = notas, y = n_i,
fill = as.factor(n_i))) +
geom_col(alpha = 0.7) +
scale_fill_manual(values = met.brewer("Klimt")) +
guides(fill = "none") +
labs(x = "Notas", y = "Frec. absolutas acumuladas",
title = "FRECUENCIAS ABSOLUTAS Y RELATIVAS")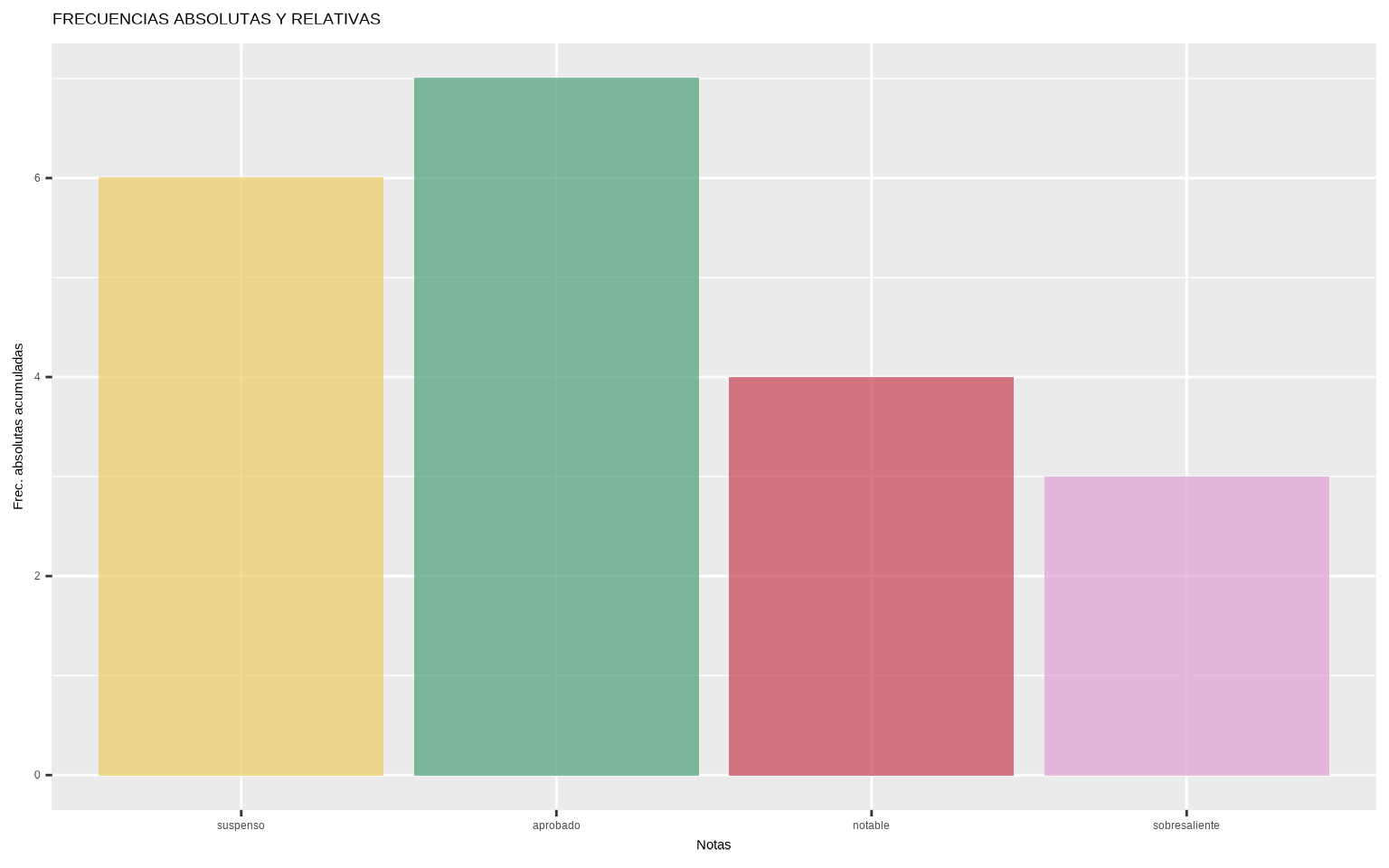
ggplot(notas_freq_acum,
aes(x = notas, y = N_i,
fill = as.factor(N_i))) +
geom_col(alpha = 0.7) +
scale_fill_manual(values = met.brewer("Klimt")) +
guides(fill = "none") +
labs(x = "Notas", y = "Frec. absolutas acumuladas",
title = "FRECUENCIAS ABSOLUTAS Y RELATIVAS")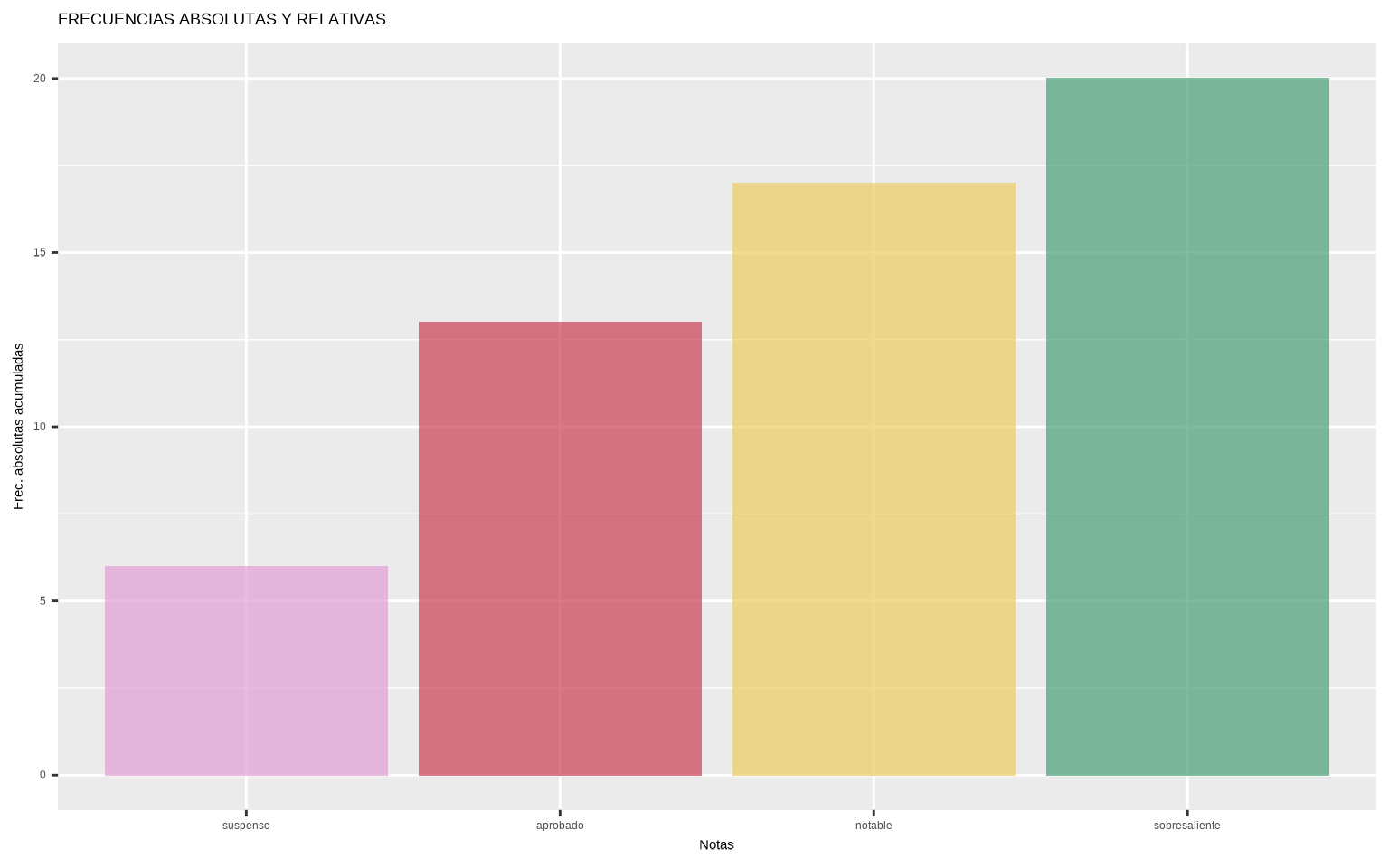
ggplot(notas_freq_acum,
aes(x = notas, y = F_i,
fill = as.factor(F_i))) +
geom_col(alpha = 0.7) +
scale_fill_manual(values = met.brewer("Klimt")) +
guides(fill = "none") +
labs(x = "Notas", y = "Frec. relativas acumuladas",
title = "FRECUENCIAS ABSOLUTAS Y RELATIVAS")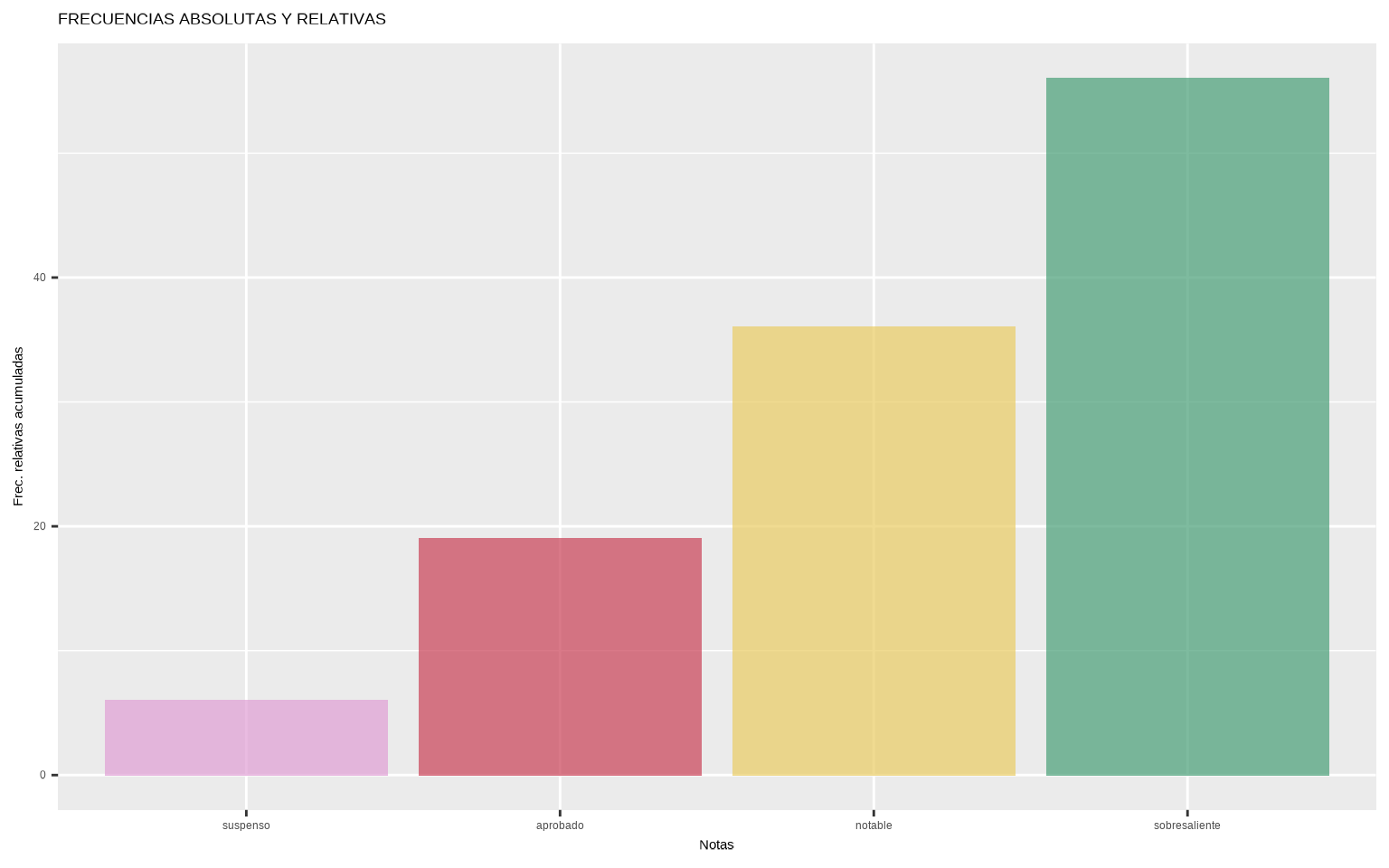
Puedes ampliar sobre cómo recategorizar variables continuas en ordinales en 19 Depuración y transformación
23.4 📝 Ejercicios
(haz click en las flechas para ver soluciones)
📝Ejercicio 1: usando dplyr de
{tidvyerse} calcula la tabla de frecuencias absolutas de la variableskin_color del conjunto de datos de starwars.
- Solución:
## # A tibble: 31 × 2
## skin_color n
## <chr> <int>
## 1 blue 2
## 2 blue, grey 2
## 3 brown 4
## 4 brown mottle 1
## 5 brown, white 1
## 6 dark 6
## 7 fair 17
## 8 fair, green, yellow 1
## 9 gold 1
## 10 green 6
## # … with 21 more rows
📝Ejercicio 2: repite el ejercicio anterior pero reagrupa los niveles poco frecuentes (poco frecuente definido como que aparezca dos o menos veces) con
fct_lump_min().
- Solución:
## # A tibble: 8 × 2
## fskin_color n
## <fct> <int>
## 1 brown 4
## 2 dark 6
## 3 fair 17
## 4 green 6
## 5 grey 6
## 6 light 11
## 7 pale 5
## 8 Other 32
📝Ejercicio 3: añade a la tabla anterior la tabla de frecuencias relativas de la columna
skin_color.
- Solución:
freq_skin <-
starwars %>%
mutate(fskin_color =
fct_lump_min(skin_color, min = 3)) %>%
count(fskin_color) %>%
rename(ni = n) %>%
mutate(fi = ni / sum(ni))
freq_skin## # A tibble: 8 × 3
## fskin_color ni fi
## <fct> <int> <dbl>
## 1 brown 4 0.0460
## 2 dark 6 0.0690
## 3 fair 17 0.195
## 4 green 6 0.0690
## 5 grey 6 0.0690
## 6 light 11 0.126
## 7 pale 5 0.0575
## 8 Other 32 0.368
📝Ejercicio 4: recategoriza la variable
height usando la función cut con 6 cortes (filtrando antes los valores ausentes). Formatea esa nueva columna como un factor, calculando sus frecuencias y agrupa para no tener clases con menos de 7 valores.
- Solución:
starwars_fheight <-
starwars %>%
filter(!is.na(height)) %>%
mutate(fheight = factor(cut(height, breaks = 6)))
# Frecuencias
fct_count(starwars_fheight$fheight)## # A tibble: 6 × 2
## f n
## <fct> <int>
## 1 (65.8,99] 7
## 2 (99,132] 2
## 3 (132,165] 10
## 4 (165,198] 51
## 5 (198,231] 9
## 6 (231,264] 2
# Reagrupamos
starwars_fheight <-
starwars_fheight %>%
mutate(fheight =
fct_lump_min(fheight, min = 7,
other_level = "otros"))
fct_count(starwars_fheight$fheight)## # A tibble: 5 × 2
## f n
## <fct> <int>
## 1 (65.8,99] 7
## 2 (132,165] 10
## 3 (165,198] 51
## 4 (198,231] 9
## 5 otros 4
📝Ejercicio 5: genera las frecuencias acumuladas resultantes de la columna recategorizada del ejercicio anterior.
- Solución:
freq_fheight <-
starwars_fheight %>%
count(fheight) %>%
rename(ni = n) %>%
mutate(fi = ni / sum(ni),
Ni = cumsum(ni),
Fi = cumsum(fi))
freq_fheight## # A tibble: 5 × 5
## fheight ni fi Ni Fi
## <fct> <int> <dbl> <int> <dbl>
## 1 (65.8,99] 7 0.0864 7 0.0864
## 2 (132,165] 10 0.123 17 0.210
## 3 (165,198] 51 0.630 68 0.840
## 4 (198,231] 9 0.111 77 0.951
## 5 otros 4 0.0494 81 1