Capítulo 25 Resumiendo y relacionado datos
Scripts usados:
- script25.R: resumiendo y relacionando datos. Ver en https://github.com/dadosdelaplace/courses-ECI-2022/blob/main/scripts/script25.R
Ahora que ya sabemos depurar y transformar los datos, y algunas de las características de los tipos de variables, en esta sección vamos a aprender dos cosas básicas a la hora de trabajar con datos:
- Realizar resúmenes numéricos de los datos, de forma general pero también cuando queremos calcular estadísticas desagregadas por grupos.
- Medidas de centralización, dispersión y posición
- Relacionar tablas entre sí (los famosos join).
25.1 Resúmenes numéricos (summarise y skimr) y por grupos (group_by)
Antes de pasar a ver cómo generar nuestras propias estadísticas de los datos, veamos la funcionalidad de un maravilloso paquete llamado skimr, que nos permite tener en un vistazo un resumen numérico muy completo de nuestros datos, con histograma/diagrama de barras incluido.
| Name | Piped data |
| Number of rows | 87 |
| Number of columns | 14 |
| _______________________ | |
| Column type frequency: | |
| character | 8 |
| list | 3 |
| numeric | 3 |
| ________________________ | |
| Group variables | None |
Variable type: character
| skim_variable | n_missing | complete_rate | min | max | empty | n_unique | whitespace |
|---|---|---|---|---|---|---|---|
| name | 0 | 1.00 | 3 | 21 | 0 | 87 | 0 |
| hair_color | 5 | 0.94 | 4 | 13 | 0 | 12 | 0 |
| skin_color | 0 | 1.00 | 3 | 19 | 0 | 31 | 0 |
| eye_color | 0 | 1.00 | 3 | 13 | 0 | 15 | 0 |
| sex | 4 | 0.95 | 4 | 14 | 0 | 4 | 0 |
| gender | 4 | 0.95 | 8 | 9 | 0 | 2 | 0 |
| homeworld | 10 | 0.89 | 4 | 14 | 0 | 48 | 0 |
| species | 4 | 0.95 | 3 | 14 | 0 | 37 | 0 |
Variable type: list
| skim_variable | n_missing | complete_rate | n_unique | min_length | max_length |
|---|---|---|---|---|---|
| films | 0 | 1 | 24 | 1 | 7 |
| vehicles | 0 | 1 | 11 | 0 | 2 |
| starships | 0 | 1 | 17 | 0 | 5 |
Variable type: numeric
| skim_variable | n_missing | complete_rate | mean | sd | p0 | p25 | p50 | p75 | p100 | hist |
|---|---|---|---|---|---|---|---|---|---|---|
| height | 6 | 0.93 | 174.36 | 34.77 | 66 | 167.0 | 180 | 191.0 | 264 | ▁▁▇▅▁ |
| mass | 28 | 0.68 | 97.31 | 169.46 | 15 | 55.6 | 79 | 84.5 | 1358 | ▇▁▁▁▁ |
| birth_year | 44 | 0.49 | 87.57 | 154.69 | 8 | 35.0 | 52 | 72.0 | 896 | ▇▁▁▁▁ |
Dicho resumen nos proporciona:
Variables de tipo caracter:
n_missing(número de ausentes),complete_rate(proporción de datos sin ausentes),min/maxyn_unique(número de valores únicos).Variables de tipo lista:
n_missing(número de ausentes),complete_rate(proporción de datos sin ausentes),n_unique(número de valores únicos) ymin_length/max_length(longitud mínimo/máxima de las listas).Variables de tipo numérico:
n_missing(número de ausentes),complete_rate(proporción de datos sin ausentes),mean/sd(media y cuasidesviación típica),p0/p25/p50/p75/p100(cuartiles, percentiles 0%-25%-50%-75%-100%, valores que nos dividen nuestro conjunto en 4 trozos) ehist(una especie de histograma/barras sencillo).
Este resumen no solo podemos visualizarlo sino que podemos guardarlo para exportarlo por ejemplo en un .csv. Sin embargo, aunque el resumen es bastante completo, muchas veces querremos generar nuestras propias estadísticas o resúmenes numéricos, y para eso vamos a aplicar summarise(), que nos calculará estadísticas de nuestros datos.
25.1.1 Medidas de centralización y dispersión
Por ejemplo, vamos a calcular las medidas de centralización (media-mediana-moda). Para la media y la mediana basta con usar las funciones correspondientes mean() y median(), dentro de summarise()
## # A tibble: 1 × 2
## media mediana
## <dbl> <dbl>
## 1 NA NAAl contrario que las demás órdenes de tidyverse, la función summarise() no nos devuelve la tabla original modificada, sino un resumen de los datos, con las funciones que le hayamos indicdo. Como ves nos devuelve un dato ausente ya que al existir datos ausentes en la variables, la media también lo es. Para evitar ese problema podemos hacer dos cosas: eliminar antes los ausentes, o indicarle en la propia media y mediana que haga el cálculo ignorando los valores NA.
# Primero eliminamos NA
starwars %>% drop_na(mass) %>%
summarise(media = mean(mass), mediana = median(mass))## # A tibble: 1 × 2
## media mediana
## <dbl> <dbl>
## 1 97.3 79
# Al realizar el cálculo los ignora
starwars %>%
summarise(media = mean(mass, na.rm = TRUE),
mediana = median(mass, na.rm = TRUE))## # A tibble: 1 × 2
## media mediana
## <dbl> <dbl>
## 1 97.3 79Las medidas de centralización son aquellos parámetros o valores que nos informe en torno a que valores se concentran los datos. La media\(\overline{x}\) es una medida de centralización basada en el valor que nos minimiza el promedio de desviaciones al cuadrado: la media es el valor que está más cerca de todos los puntos a la vez (con la distancia Euclídea, definida como la diferencia al cuadrado)
\[\overline{x} = \frac{1}{N} \sum_{i=1}^{N} x_i, \qquad \overline{x} = \arg \min_{x} \frac{1}{N} \sum_{i=1}^{N} \left(x_i - x \right)^2\]
La media solo se puede calcular para variables cuantitativas: solo podemos calcular medias de números.
# Media de todas las cuantitativas
starwars_nueva %>%
summarise(media = across(where(is.numeric), mean, na.rm = TRUE))## # A tibble: 1 × 1
## media$height $mass $birth_year $n_films
## <dbl> <dbl> <dbl> <dbl>
## 1 174. 97.3 87.6 1.99
La mediana se define como el valor que ocupa el centro de los datos cuando los ordenamos de menor a mayor, un valor que nos deja por debajo al menos el 50% y por encima al menos el 50%.
# Media y mediana de todas las cuantitativas
starwars_nueva %>%
summarise(media = across(where(is.numeric), mean, na.rm = TRUE),
mediana = across(where(is.numeric), median, na.rm = TRUE))## # A tibble: 1 × 2
## media$height $mass $birth_year $n_films mediana$height $mass $birth_year
## <dbl> <dbl> <dbl> <dbl> <int> <dbl> <dbl>
## 1 174. 97.3 87.6 1.99 180 79 52La mediana también se puede calcular para variables cualitativas ordinales (categorías que se puedan ordenar), además de para variables cuantitativas.. Vamos a construir una variable que sea «muy bajo-bajo-medio-alto-muy alto» según la estatura, y calcular la mediana para dichas categorías.
categorias <- c("muy bajo", "bajo", "medio", "alto", "muy alto")
starwars_talla <-
starwars %>%
mutate(talla =
cut(height, breaks = c(-Inf, 80, 120, 160, 190, Inf),
labels = categorias))
# Mediana (hay que pasárselo como número)
starwars_talla %>%
summarise(mediana =
categorias[median(as.numeric(talla), na.rm = TRUE)])## # A tibble: 1 × 1
## mediana
## <chr>
## 1 altoPara la moda tenemos algún problema mayor ya que no hay un función en los paquetes {base} para su cálculo directo. La moda se define como el valor más repetido: si tenemos algo discreto o cualitativo es la barra más alta.
library(tidyverse)
# Carga
netflix <-
read_csv('https://raw.githubusercontent.com/elartedeldato/datasets/main/netflix_titles.csv')
# Películas y series de insti
netflix_hs <- netflix %>%
filter(str_detect(toupper(description), "HIGH SCHOOL"))
netflix_hs ## # A tibble: 150 × 12
## show_id type title director cast country date_added release_year rating
## <chr> <chr> <chr> <chr> <chr> <chr> <chr> <dbl> <chr>
## 1 s8 Movie 187 Kevin R… Samuel… United… November … 1997 R
## 2 s32 Movie #Frien… Rako Pr… Adipat… Indone… May 21, 2… 2018 TV-G
## 3 s34 Movie #reali… Fernand… Nesta … United… September… 2017 TV-14
## 4 s47 Movie 1 Chan… Adam De… Lexi G… United… July 1, 2… 2014 TV-PG
## 5 s48 Movie 1 Mile… Leif Ti… Billy … United… July 7, 2… 2017 TV-14
## 6 s56 Movie 100 Th… <NA> Isabel… United… November … 2014 TV-Y
## 7 s58 Movie 100% H… Jastis … Anisa … Indone… January 7… 2020 TV-14
## 8 s148 Movie A Baby… Rachel … Tamara… United… October 1… 2020 TV-PG
## 9 s251 Movie A Walk… Adam Sh… Mandy … United… July 1, 2… 2002 PG
## 10 s297 Movie Across… Julien … Sarah … Canada April 1, … 2015 TV-MA
## # … with 140 more rows, and 3 more variables: duration <chr>, listed_in <chr>,
## # description <chr>
# Manipulamos fechas
library(lubridate)
netflix_final <-
netflix_hs %>%
mutate(year = year(mdy(date_added))) %>%
filter(!is.na(year))
netflix_resumen <-
netflix_final %>%
group_by(year) %>%
count() %>%
ungroup()
library(sysfonts)
library(showtext)
font_add_google(family = "Bebas Neue", name = "Bebas Neue")
font_add_google(family = "Permanent Marker", name = "Permanent Marker")
showtext_auto()
ggplot(netflix_resumen, aes(x = year, y = n)) +
geom_col(fill = "red") +
scale_x_continuous(breaks = netflix_resumen$year) +
theme_void() +
theme(legend.position = "none",
plot.title = element_text(family = "Bebas Neue",
color = "red", size = 80)) +
labs(title = "NETFLIX",
subtitle = "Películas y series de instituto",
caption = "Basada en El Arte del Dato (https://elartedeldato.com) | Datos: Kaggle") +
theme(panel.background = element_rect(fill = "black"),
plot.background = element_rect(fill = "black",
color = "black"),
panel.grid.major.y =
element_line(size = 0.1, color = "white"),
plot.subtitle = element_text(family = "Permanent Marker",
size = 21, color = "white"),
plot.caption = element_text(family = "Permanent Marker",
color = "white", size = 19),
axis.text =
element_text(size = 15, family = "Permanent Marker",
color = "white"),
plot.margin = margin(t = 4, r = 4, b = 4, l = 8, "pt")) +
annotate("text", label = "Moda",
x = 2020.7, y = 47, hjust = 0.2, vjust = 0, family = "Permanent Marker", size = 6, color = 'white', angle = 10) +
annotate("curve", x = 2020.3, y = 48, xend = 2020, yend = 44,
color = "white")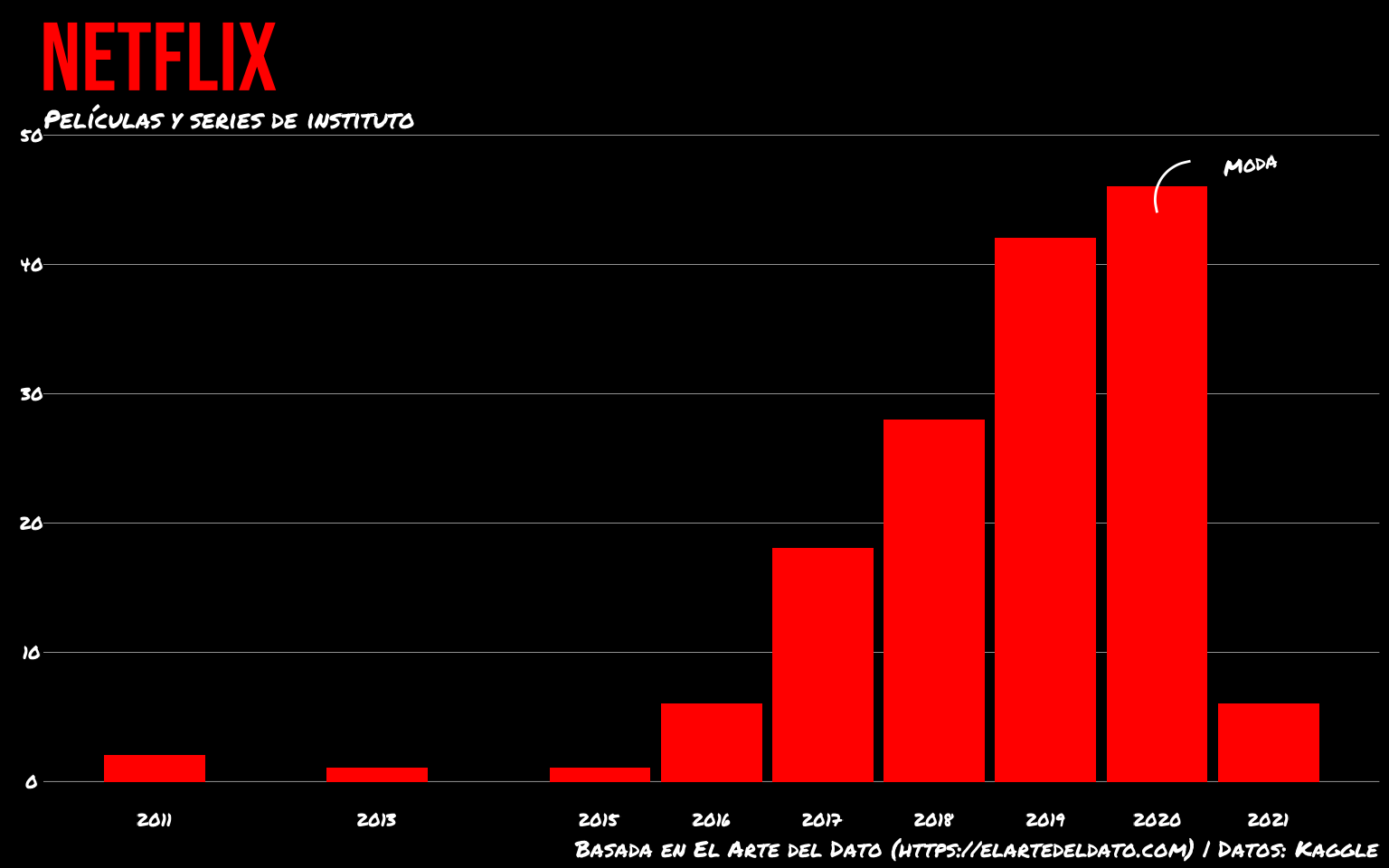
Para calcularla podemos usar el paquete modeest: la función mfv() nos calcula la moda exacta de una variable numérica discreta o cuantitativa (busca los valores más repetidos), la función mlv() nos calcula la moda estimada de una variable numérica continua.
library(modeest)
# Media y mediana y moda de mass y n_films
resumen <-
starwars_nueva %>%
summarise(media = across(c(mass, n_films), mean, na.rm = TRUE),
mediana = across(c(mass, n_films), median, na.rm = TRUE),
moda_n_films = mfv(n_films, na_rm = TRUE),
moda_mass = mlv(mass, na.rm = TRUE))
resumen## # A tibble: 1 × 4
## media$mass $n_films mediana$mass $n_films moda_n_films moda_mass
## <dbl> <dbl> <dbl> <int> <int> <dbl>
## 1 97.3 1.99 79 1 1 80.3Fíjate que el resumen ha agrupado todas las modas y medianas que hemos calculado a la vez: la salida de nuestro resumen es una lista, con tablas a su vez dentro.
Veamos un ejemplo sintético de distribuciones multimodales, generando con rnorm() (genera datos aleatorias provenientes de una distribución normal) un conjunto unimodal, bimodal y trimodal, los 3 con la misma media.
n <- 900
# Datos
datos <-
tibble("unimod" = rnorm(n, 5, 1),
"bimod" = c(rnorm(n/2, 3, 1), rnorm(n/2, 7, 1)),
"trimod" = c(rnorm(n/3, 2, 1), rnorm(n/3, 5, 1),
rnorm(n/3, 8, 1)))
# Tidy data
datos <-
pivot_longer(datos, cols = everything(),
names_to = "tipo", values_to = "values")
# Estadisticas
datos %>%
group_by(tipo) %>%
summarise(media = mean(values),
mediana = median(values))## # A tibble: 3 × 3
## tipo media mediana
## <chr> <dbl> <dbl>
## 1 bimod 5.00 5.14
## 2 trimod 5.00 5.05
## 3 unimod 4.94 4.94Sólo utilizando la media estos casos son indistiguibles, ya que en todos los casos la media y mediana coinciden, pero si podemos hacerlo visualizando sus densidades.
library(ggridges)
ggplot(datos,
aes(y = tipo, x = values, fill = tipo)) +
geom_density_ridges(alpha = 0.7, height = 1) +
scale_fill_manual(values = met.brewer("Klimt")) +
labs(fill = "Distribución",
y = "Distribución",
title = "DISTRIBUCIONES MULTIMODALES")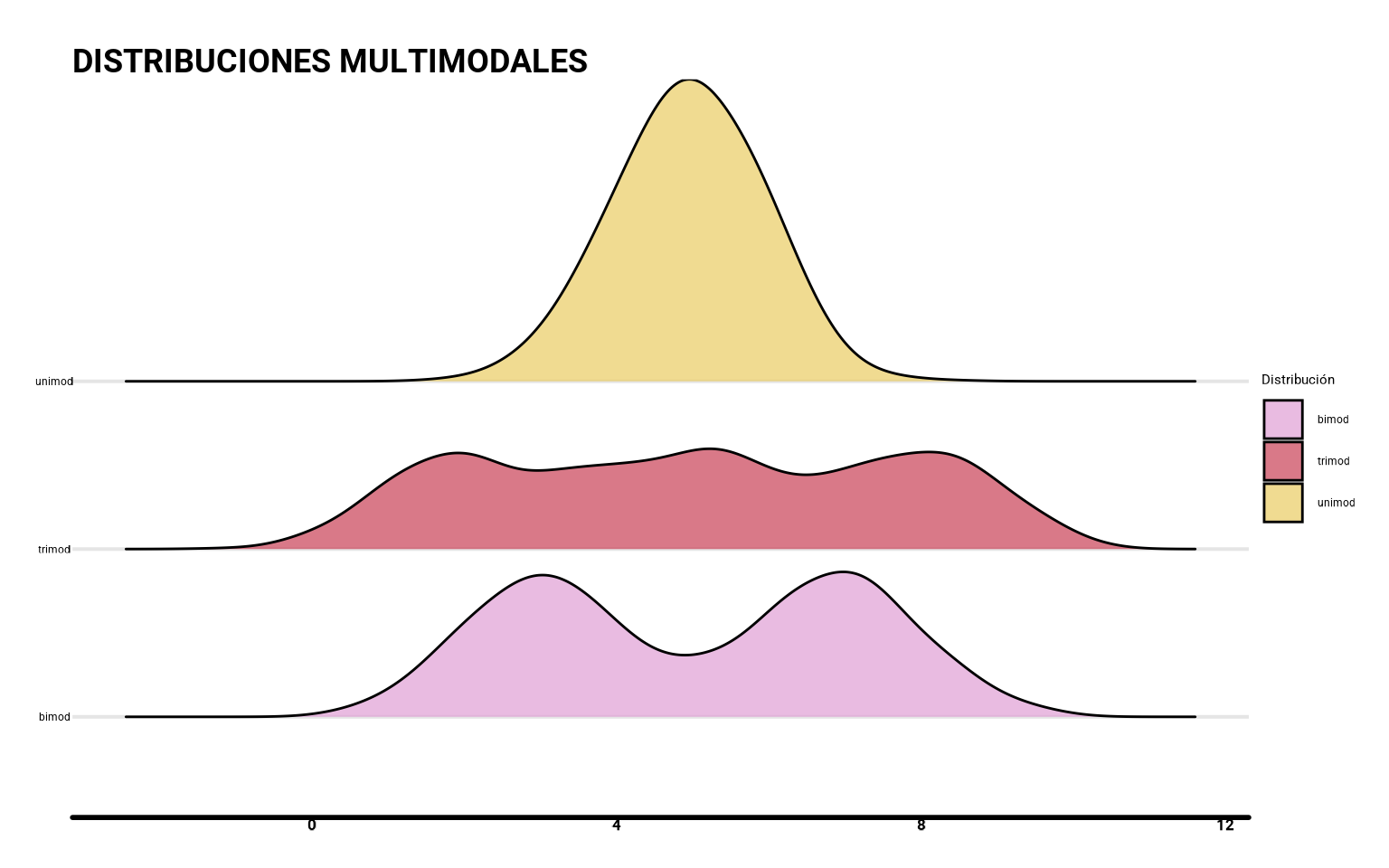
Con stat_density_ridges() podemos además marcar algunos valores, como por ejemplo los cuartiles.
ggplot(datos,
aes(y = tipo, x = values, fill = tipo)) +
geom_density_ridges(alpha = 0.7, height = 1) +
stat_density_ridges(quantile_lines = TRUE,
quantiles = c(0.25, 0.5, 0.75),
color = "black", alpha = .8,
size = 0.7) +
scale_fill_manual(values = met.brewer("Klimt")) +
labs(fill = "Distribución",
y = "Distribución",
title = "DISTRIBUCIONES MULTIMODALES")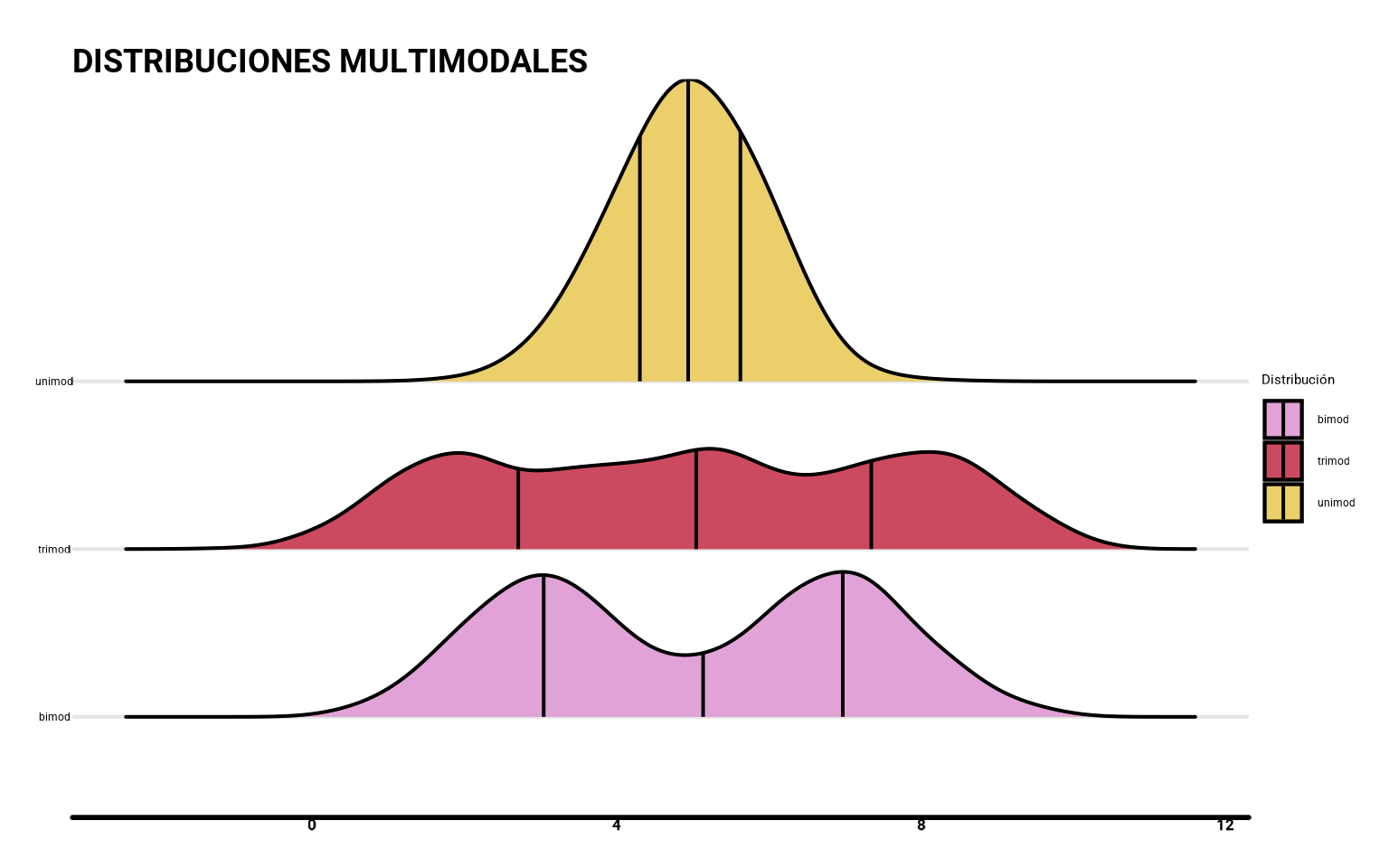
De la misma manera podemos pedirle que nos calcule medidas de dispersión (varianza, desv. típica y cv), que nos indican cómo de dispersos están los datos respecto a un centro, normalmente la media, y medidas de localización (percentiles) (valores que nos parten los datos en trozos iguales). Dada una proporción de los datos \(0 < p < 1\), el cuantil de orden \(p\) de una variable cuantitativa, denotado como \(Q_p\), es el valor más pequeño tal que su frecuencia relativa acumulada es mayor o igual que \(p\): es el número más pequeño que deja a su izquierda (incluyéndolo a él) como mínimo la fracción \(p\) de los datos (la propia mediana es el cuantil \(Q_{0.5}\).
starwars %>%
summarise(media = mean(mass, na.rm = TRUE),
mediana = median(mass, na.rm = TRUE),
moda = mlv(mass, na.rm = TRUE),
var = var(mass, na.rm = TRUE),
sd = sd(mass, na.rm = TRUE),
cv = sd / abs(media),
p13 = quantile(mass, probs = c(0.13), na.rm = TRUE),
p87 = quantile(mass, probs = c(0.87), na.rm = TRUE))## # A tibble: 1 × 8
## media mediana moda var sd cv p13 p87
## <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl>
## 1 97.3 79 80.3 28716. 169. 1.74 46.6 111.Haciendo uso de cosas ya vistas podemos, por ejemplo, calcular el coeficiente de variación (CV) de todas las variables numéricas para poder decidir cual es más o menos dispersa.
resumen <-
starwars %>%
summarise(media = across(where(is.numeric), mean, na.rm = TRUE),
var = across(where(is.numeric), var, na.rm = TRUE),
cv = sqrt(var) / abs(media))
resumen$media## # A tibble: 1 × 3
## height mass birth_year
## <dbl> <dbl> <dbl>
## 1 174. 97.3 87.6
resumen$var## # A tibble: 1 × 3
## height mass birth_year
## <dbl> <dbl> <dbl>
## 1 1209. 28716. 23929.
resumen$cv # más homogénea la altura por tener menos CV.## height mass birth_year
## 1 0.1994197 1.741382 1.76658725.1.2 Agrupando datos: group_by
Una de las funcionalidades más potentes es la opción de añadir antes una agrupación con group_by(). Esta función per se no cambia los datos sino que cambia la forma en la que se aplicarán las funciones posteriores, realizándose por desagregadas grupos.
Imagina que queremos calcular la media de altura y peso de cada personaje PERO desagregada por cada una de las clases que tenemos en la variable sex.
starwars %>% group_by(sex) %>%
summarise(media_altura = mean(height, na.rm = TRUE),
media_peso = mean(mass, na.rm = TRUE)) %>%
ungroup()## # A tibble: 5 × 3
## sex media_altura media_peso
## <chr> <dbl> <dbl>
## 1 female 169. 54.7
## 2 hermaphroditic 175 1358
## 3 male 179. 81.0
## 4 none 131. 69.8
## 5 <NA> 181. 48Lo que obtenemos no es la media de todos los personajes sino la media desagregada por grupo, grupo marcado por la variable sex. Las agrupaciones pueden estar en función de varias variables a la vez.
starwars %>% group_by(sex, gender) %>%
summarise(media_altura = mean(height, na.rm = TRUE),
media_peso = mean(mass, na.rm = TRUE)) %>%
ungroup()## # A tibble: 6 × 4
## sex gender media_altura media_peso
## <chr> <chr> <dbl> <dbl>
## 1 female feminine 169. 54.7
## 2 hermaphroditic masculine 175 1358
## 3 male masculine 179. 81.0
## 4 none feminine 96 NaN
## 5 none masculine 140 69.8
## 6 <NA> <NA> 181. 48Dicha función también es muy útil cuando queremos realizar un filtro de registros en base al número de cada clase: por ejemplo, vamos a filtrar los registros que pertenezcan a una clase de sex que tenga al menos 10 individuos dentro de dicho grupo.
## # A tibble: 5 × 2
## sex n
## <chr> <int>
## 1 female 16
## 2 hermaphroditic 1
## 3 male 60
## 4 none 6
## 5 <NA> 4Si te fijas solo deberíamos filtrar los registros que sean female y male. Vamos a hacerlo de forma automática en base a dicho umbral.
# Podemos filtrar por grupos solo aquellos que superen un
# un umbral mínimo
starwars %>%
group_by(sex) %>%
filter(n() > 10) %>%
ungroup()## # A tibble: 76 × 14
## name height mass hair_color skin_color eye_color birth_year sex gender
## <chr> <int> <dbl> <chr> <chr> <chr> <dbl> <chr> <chr>
## 1 Luke S… 172 77 blond fair blue 19 male mascu…
## 2 Darth … 202 136 none white yellow 41.9 male mascu…
## 3 Leia O… 150 49 brown light brown 19 fema… femin…
## 4 Owen L… 178 120 brown, grey light blue 52 male mascu…
## 5 Beru W… 165 75 brown light blue 47 fema… femin…
## 6 Biggs … 183 84 black light brown 24 male mascu…
## 7 Obi-Wa… 182 77 auburn, wh… fair blue-gray 57 male mascu…
## 8 Anakin… 188 84 blond fair blue 41.9 male mascu…
## 9 Wilhuf… 180 NA auburn, gr… fair blue 64 male mascu…
## 10 Chewba… 228 112 brown unknown blue 200 male mascu…
## # … with 66 more rows, and 5 more variables: homeworld <chr>, species <chr>,
## # films <list>, vehicles <list>, starships <list>Para comprobar rápidamente que efectivamente solo ha filtrado aquellos grupos con más de 10 elementos en ellos podemos añadir count().
## # A tibble: 2 × 2
## sex n
## <chr> <int>
## 1 female 16
## 2 male 60Los resúmenes y las agrupaciones podemos combinarlas de todas las formas que nos imaginemos, por ejemplo, calculando la media desagregada por sexo y género pero solo de las variables numéricas.
starwars %>% # doble agrupación
group_by(sex, gender) %>%
summarise(across(where(is.numeric), mean, na.rm = TRUE)) %>%
ungroup()## # A tibble: 6 × 5
## sex gender height mass birth_year
## <chr> <chr> <dbl> <dbl> <dbl>
## 1 female feminine 169. 54.7 47.2
## 2 hermaphroditic masculine 175 1358 600
## 3 male masculine 179. 81.0 85.5
## 4 none feminine 96 NaN NaN
## 5 none masculine 140 69.8 53.3
## 6 <NA> <NA> 181. 48 6225.1.3 Rowwise: operaciones por filas
Por último veamos un ejemplo de una opción muy útil usada antes de una operación que es rowwise(): toda operación que venga después se aplicará en cada fila por separado. Para el ejemplo vamos a definir un fichero dummy de notas en mates, lengua y dibujo de 50 alumnos. Para ello usamos la función sample(): le decimos que seleccione aleatoriamente size = 50 notas de un conjunto de notas posibles (0:10), y que lo haga con reemplazamiento (replace = TRUE, es decir, que dos alumnos puedan tener la misma nota)
notas <- tibble("mates" = sample(0:10, size = 50, replace = TRUE),
"lengua" = sample(0:10, size = 50, replace = TRUE),
"dibujo" = sample(0:10, size = 50, replace = TRUE))
notas## # A tibble: 50 × 3
## mates lengua dibujo
## <int> <int> <int>
## 1 3 10 7
## 2 0 3 6
## 3 9 6 3
## 4 1 7 1
## 5 1 0 1
## 6 3 10 6
## 7 4 4 10
## 8 0 9 4
## 9 8 2 0
## 10 2 3 10
## # … with 40 more rowsUna vez que tenemos 3 notas aleatorias por cada uno de los 50 alumnos, ¿qué sucede si yo quiero calcular la nota media del curso?
## # A tibble: 50 × 4
## mates lengua dibujo media_curso
## <int> <int> <int> <dbl>
## 1 3 10 7 4.77
## 2 0 3 6 4.77
## 3 9 6 3 4.77
## 4 1 7 1 4.77
## 5 1 0 1 4.77
## 6 3 10 6 4.77
## 7 4 4 10 4.77
## 8 0 9 4 4.77
## 9 8 2 0 4.77
## 10 2 3 10 4.77
## # … with 40 more rowsComo ves si aplicamos la media de las tres variables, en cada fila el valor de media_curso es idéntico ya que nos ha hecho la media global: ha tomado las 50 filas, las 3 columnas, y ha hecho la media de 150 datos. Cuando en realidad a nosotros nos gustaría sacar una media por registro, que para cada alumno tengamos la media de las asignaturas.
## # A tibble: 50 × 4
## # Rowwise:
## mates lengua dibujo media_curso
## <int> <int> <int> <dbl>
## 1 3 10 7 6.67
## 2 0 3 6 3
## 3 9 6 3 6
## 4 1 7 1 3
## 5 1 0 1 0.667
## 6 3 10 6 6.33
## 7 4 4 10 6
## 8 0 9 4 4.33
## 9 8 2 0 3.33
## 10 2 3 10 5
## # … with 40 more rowsSolos nos falta poner la guinda a lo aprendido a esta introducción: vamos a ver como podemos relacionar dos conjuntos de datos distintos entre sí.
25.2 Relacionar datos (joins)
Una de las opciones más comunes para trabajar con datos es tener a nuestra disposición diversas tablas, con alguno o varios de los campos en común, y nos interesa a veces cruzar datos de ambos para tener una información más completa con el conjunto de las tablas. Es lo que se conoce en ciencia de datos e informática como hacer un join de tablas. Para ese cruce será indispensable que haya uno o varios campos clave, campos que sirvan para identificar unívocamente cada registro (por ejemplo, DNI).
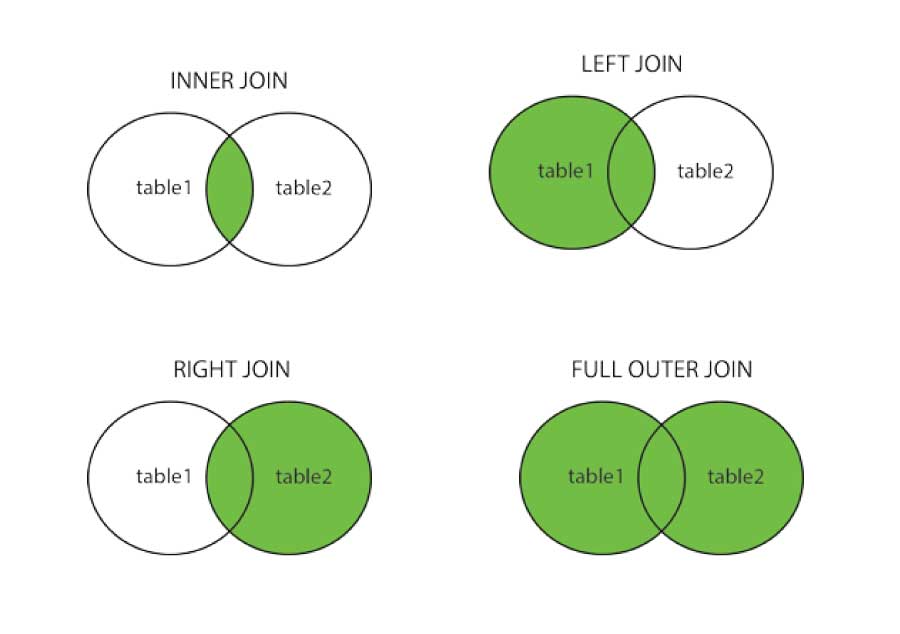
Imagen/gráfica 25.1: Esquema con los principales tipos de join, extraído de https://estradawebgroup.com/Post/-Que-es-y-para-que-sirve-SQL-Joins-/4278
Existen principalmente cuatro tipos de cruces si pensamos en cruzar un conjunto A con otro conjunto B:
Inner join: solo nos quedamos con las filas que tengan correspondencia en ambas tablas (personas cuyo DNI aparezca en ambas tablas, por ejemplo).
Left (outer) join: nos quedamos con todas las filas de
A, buscando que registros de dicha tabla están también enB, completando los datos de esta tabla para esos registros.Right (outer) join: nos quedamos con todas las filas de
B, buscando que registros de dicha tabla están también enA, completando los datos de esta tabla para esos registros.Full join: nos quedamos con todas las filas de
AyB, tengan o no correspondencia en la otra tabla (si no está en una de ellas, las columnas correspondientes quedarán como campo ausente).
Esos campos clave (keys) serán las columnas que usaremos para definir los cruces. Para los ejemplos usaremos las tablas del paquete nycflights13.
Dicho paquete cuenta con las siguientes tablas:
-
airlines: nombre de la aerolínea (con su abreviatura). -
airports: datos de aeropuertos (nombres, longitud, latitud, altitud, etc). -
flights: datos de vuelos (contailnumcomo marca de idenfiticación). -
planes: datos de los aviones. -
weather: datos meteorológicos horarios de las estaciones LGA, JFK y EWR.
Veamos un ejemplo: imagina que queremos completar en la tabla de vuelos los datos de cada una de las aerolíneas que operan dichos vuelos. Vamos a seleccionar unas pocas columnas para que sea más fácil de visualizar.
# Seleccionamos antes columnas para que sea más corto
flights_filtrada <- flights %>%
select(year:day, arr_time, carrier:dest)
flights_filtrada## # A tibble: 336,776 × 9
## year month day arr_time carrier flight tailnum origin dest
## <int> <int> <int> <int> <chr> <int> <chr> <chr> <chr>
## 1 2013 1 1 830 UA 1545 N14228 EWR IAH
## 2 2013 1 1 850 UA 1714 N24211 LGA IAH
## 3 2013 1 1 923 AA 1141 N619AA JFK MIA
## 4 2013 1 1 1004 B6 725 N804JB JFK BQN
## 5 2013 1 1 812 DL 461 N668DN LGA ATL
## 6 2013 1 1 740 UA 1696 N39463 EWR ORD
## 7 2013 1 1 913 B6 507 N516JB EWR FLL
## 8 2013 1 1 709 EV 5708 N829AS LGA IAD
## 9 2013 1 1 838 B6 79 N593JB JFK MCO
## 10 2013 1 1 753 AA 301 N3ALAA LGA ORD
## # … with 336,766 more rowsQueremos TODAS las filas de los vuelos, todos sus registros, pero añadiendo la información que tenemos de la aerolínea que opere los vuelos, así que haremos un LEFT JOIN de flights vs airlines. El campo común que nos permite cruzarla, la clave (key) es el código abreviado de las aerolíneas (variable carrier).
# Mismas filas pero con una nueva columna: siempre que sea
# posible el cruce tendrá la info de la aerolínea
l_join_flights_airlines <-
flights_filtrada %>% left_join(airlines, by = "carrier")
l_join_flights_airlines## # A tibble: 336,776 × 10
## year month day arr_time carrier flight tailnum origin dest name
## <int> <int> <int> <int> <chr> <int> <chr> <chr> <chr> <chr>
## 1 2013 1 1 830 UA 1545 N14228 EWR IAH United Air Li…
## 2 2013 1 1 850 UA 1714 N24211 LGA IAH United Air Li…
## 3 2013 1 1 923 AA 1141 N619AA JFK MIA American Airl…
## 4 2013 1 1 1004 B6 725 N804JB JFK BQN JetBlue Airwa…
## 5 2013 1 1 812 DL 461 N668DN LGA ATL Delta Air Lin…
## 6 2013 1 1 740 UA 1696 N39463 EWR ORD United Air Li…
## 7 2013 1 1 913 B6 507 N516JB EWR FLL JetBlue Airwa…
## 8 2013 1 1 709 EV 5708 N829AS LGA IAD ExpressJet Ai…
## 9 2013 1 1 838 B6 79 N593JB JFK MCO JetBlue Airwa…
## 10 2013 1 1 753 AA 301 N3ALAA LGA ORD American Airl…
## # … with 336,766 more rowsSi te fijas ahora tenemos en l_join_flights_airlines las mismas 336776 filas pero con una columna más: la tabla airlines tenía 2 columnas, una la común con flights y en otra la nueva que se ha incorporado a la tabla. ¿Y si en flights había algún vuelo operado por alguna aerolínea que no estuviese en airlines?
## # A tibble: 0 × 10
## # … with 10 variables: year <int>, month <int>, day <int>, arr_time <int>,
## # carrier <chr>, flight <int>, tailnum <chr>, origin <chr>, dest <chr>,
## # name <chr>En este caso todos los registros de la primera tabla tenían su correspondencia en la segunda tabla. Veamos un ejemplo donde suceda eso, quitándole algunas filas a airlines, quitando las aerolíneas con códigos "B6".
airlines_filtrada <- airlines %>%
filter(!(carrier %in% c("B6")))
l_join <- flights_filtrada %>% left_join(airlines_filtrada, by = "carrier")
dim(l_join %>% filter(is.na(name)))## [1] 54635 10En el anterior ejemplo tenemos 54 635 filas que cuyo nombre está ausente, es decir, 54 635 filas de flights que no tienen correspondencia en la tabla filtrada airlines_filtrada. Ahora las filas que no han encontrado su match en la segunda tabla están como campo ausente.
l_join## # A tibble: 336,776 × 10
## year month day arr_time carrier flight tailnum origin dest name
## <int> <int> <int> <int> <chr> <int> <chr> <chr> <chr> <chr>
## 1 2013 1 1 830 UA 1545 N14228 EWR IAH United Air Li…
## 2 2013 1 1 850 UA 1714 N24211 LGA IAH United Air Li…
## 3 2013 1 1 923 AA 1141 N619AA JFK MIA American Airl…
## 4 2013 1 1 1004 B6 725 N804JB JFK BQN <NA>
## 5 2013 1 1 812 DL 461 N668DN LGA ATL Delta Air Lin…
## 6 2013 1 1 740 UA 1696 N39463 EWR ORD United Air Li…
## 7 2013 1 1 913 B6 507 N516JB EWR FLL <NA>
## 8 2013 1 1 709 EV 5708 N829AS LGA IAD ExpressJet Ai…
## 9 2013 1 1 838 B6 79 N593JB JFK MCO <NA>
## 10 2013 1 1 753 AA 301 N3ALAA LGA ORD American Airl…
## # … with 336,766 more rows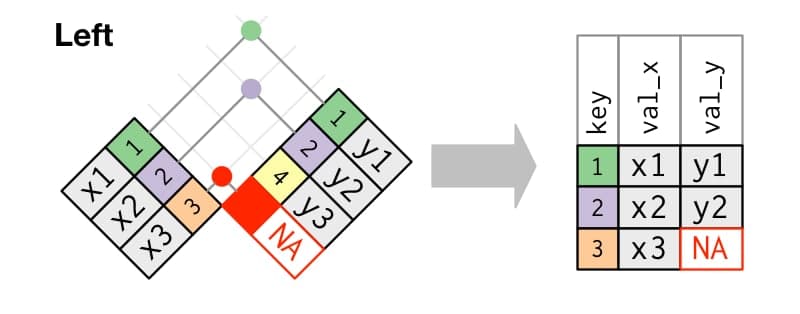
Imagen/gráfica 25.2: Esquema del left join, extraído de https://r4ds.had.co.nz/relational-data.html#mutating-joins
La misma lógica para los RIGHT JOIN y los FULL JOIN. En este último tendremos bastantes datos ausentes, ya que todos los registros que no estén en ambas tablas tendrán una parte de sus variables como NA
tabla1 <- tibble("key_1" = 1:7, "valor_1" = paste0("x", 1:7))
tabla2 <- tibble("key_2" = c(0, 1, 2, 5, 6, 9, 10),
"valor_2" = paste0("x", c(0, 1, 2, 5, 6, 9, 10)))
# Left
tabla1 %>% left_join(tabla2, by = c("key_1" = "key_2"))## # A tibble: 7 × 3
## key_1 valor_1 valor_2
## <dbl> <chr> <chr>
## 1 1 x1 x1
## 2 2 x2 x2
## 3 3 x3 <NA>
## 4 4 x4 <NA>
## 5 5 x5 x5
## 6 6 x6 x6
## 7 7 x7 <NA>
# Right
tabla1 %>% right_join(tabla2, by = c("key_1" = "key_2"))## # A tibble: 7 × 3
## key_1 valor_1 valor_2
## <dbl> <chr> <chr>
## 1 1 x1 x1
## 2 2 x2 x2
## 3 5 x5 x5
## 4 6 x6 x6
## 5 0 <NA> x0
## 6 9 <NA> x9
## 7 10 <NA> x10## # A tibble: 10 × 3
## key_1 valor_1 valor_2
## <dbl> <chr> <chr>
## 1 1 x1 x1
## 2 2 x2 x2
## 3 3 x3 <NA>
## 4 4 x4 <NA>
## 5 5 x5 x5
## 6 6 x6 x6
## 7 7 x7 <NA>
## 8 0 <NA> x0
## 9 9 <NA> x9
## 10 10 <NA> x10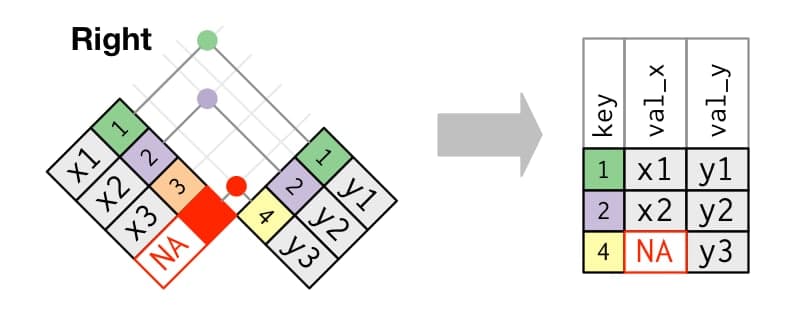
Imagen/gráfica 25.3: Esquema del right join, extraído de https://r4ds.had.co.nz/relational-data.html#mutating-joins
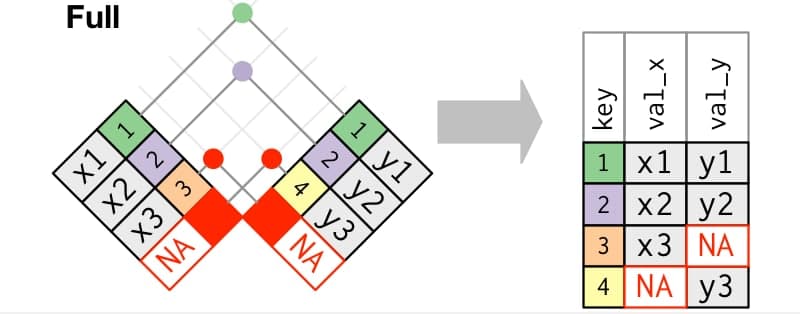
Imagen/gráfica 25.4: Esquema del full join, extraído de https://r4ds.had.co.nz/relational-data.html#mutating-joins
Un tipo de join especial son los INNER JOIN. Hasta ahora la tabla resultante tenía al menos tantas filas como tuviese la tabla más pequeña en el cruce. En el caso de los INNER JOIN vamos a reducir el tamaño ya que solo nos quedaremos con aquellos registros que podamos encontrar en ambas, de forma que el cruce nunca generará datos ausentes.
# Inner
tabla1 %>% inner_join(tabla2, by = c("key_1" = "key_2"))## # A tibble: 4 × 3
## key_1 valor_1 valor_2
## <dbl> <chr> <chr>
## 1 1 x1 x1
## 2 2 x2 x2
## 3 5 x5 x5
## 4 6 x6 x6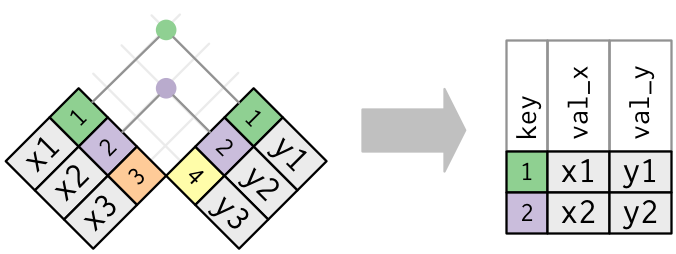
Imagen/gráfica 25.5: Esquema del inner join, extraído de https://r4ds.had.co.nz/relational-data.html#mutating-joins