Capítulo 24 Extrayendo información: estadística descriptiva con cuantitativas continuas
Scripts usados:
- script24.R: intro a la descriptiva con cuantitativas continuas. Ver en https://github.com/dadosdelaplace/courses-ECI-2022/blob/main/scripts/script24.R
Aunque hemos aprendido algunas formas de agrupar variables continuas en categorías y subintervalos, el problema es que cuando lo hacemos estamos pagando un precio: tenemos un resumen de los datos a cambio de perder información de los mismos: todos los elementos que cae en un intervalo se les imputará un único valor: la marca de clase (que normalmente es el punto medio del intervalo).
24.1 Basados en puntos
El tratamiento de las frecuencias de datos cuantitativos es similar al de los datos ordinales, excepto por un detalle: no se tienen en cuenta todos los niveles posibles, sino solo los observados.
Vamos a analizar un conjunto de datos muy interesante, que contiene las respuestas a las preguntas «¿qué probabilidad (%) asignarías al término …? Dicha pregunta se realizaó para distintos términos como «casi sin opciones» (almost no chance), «en mayor medida» (about even), «probable» (probable) o «casi seguro» (almost certainly), con el objetivo de comprender cómo la gente percibe el vocabulario relativo a la probabilidad. Los datos y gráficos han sido basados en el trabajo de Zoni Nation y data-to-viz.com
datos <-
read_csv("https://raw.githubusercontent.com/zonination/perceptions/master/probly.csv")
datos## # A tibble: 46 × 17
## `Almost Certainly` `Highly Likely` `Very Good Chanc… Probable Likely Probably
## <dbl> <dbl> <dbl> <dbl> <dbl> <dbl>
## 1 95 80 85 75 66 75
## 2 95 75 75 51 75 51
## 3 95 85 85 70 75 70
## 4 95 85 85 70 75 70
## 5 98 95 80 70 70 75
## 6 95 99 85 90 75 75
## 7 85 95 65 80 40 45
## 8 97 95 75 70 70 80
## 9 95 95 80 70 65 80
## 10 90 85 90 70 75 70
## # … with 36 more rows, and 11 more variables: We Believe <dbl>,
## # Better Than Even <dbl>, About Even <dbl>, We Doubt <dbl>, Improbable <dbl>,
## # Unlikely <dbl>, Probably Not <dbl>, Little Chance <dbl>,
## # Almost No Chance <dbl>, Highly Unlikely <dbl>, Chances Are Slight <dbl>Vamos a visualizar la media de las probabilidades asignadas para cada caso, con un diagrama de barras. Pero antes debemos de transformar el dataset a tidydata con pivot_longer().
datos_pivot <-
datos %>%
pivot_longer(cols = everything(),
names_to = "termino", values_to = "prob")
datos_pivot## # A tibble: 782 × 2
## termino prob
## <chr> <dbl>
## 1 Almost Certainly 95
## 2 Highly Likely 80
## 3 Very Good Chance 85
## 4 Probable 75
## 5 Likely 66
## 6 Probably 75
## 7 We Believe 66
## 8 Better Than Even 55
## 9 About Even 50
## 10 We Doubt 40
## # … with 772 more rowsTras ello, seleccionamos los términosAlmost No Chance, Chances Are Slight, Improbable, About Even, Probable y Almost Certainly. Además vamos a reordenar los niveles de factor de la variable termino con fct_reorder() (del paquete forcats)
datos_final <-
datos_pivot %>%
filter(termino %in% c("Almost No Chance", "Chances Are Slight",
"Improbable", "About Even",
"Probable", "Almost Certainly")) %>%
mutate(termino = fct_reorder(termino, prob))
datos_final## # A tibble: 276 × 2
## termino prob
## <fct> <dbl>
## 1 Almost Certainly 95
## 2 Probable 75
## 3 About Even 50
## 4 Improbable 20
## 5 Almost No Chance 5
## 6 Chances Are Slight 25
## 7 Almost Certainly 95
## 8 Probable 51
## 9 About Even 50
## 10 Improbable 49
## # … with 266 more rowsTras preprocesar los datos, usamos geom_col() para visualizar los datos medios.
ggplot(datos_final %>%
group_by(termino) %>%
summarise(media = mean(prob)),
aes(x = termino, y = media, fill = termino)) +
geom_col()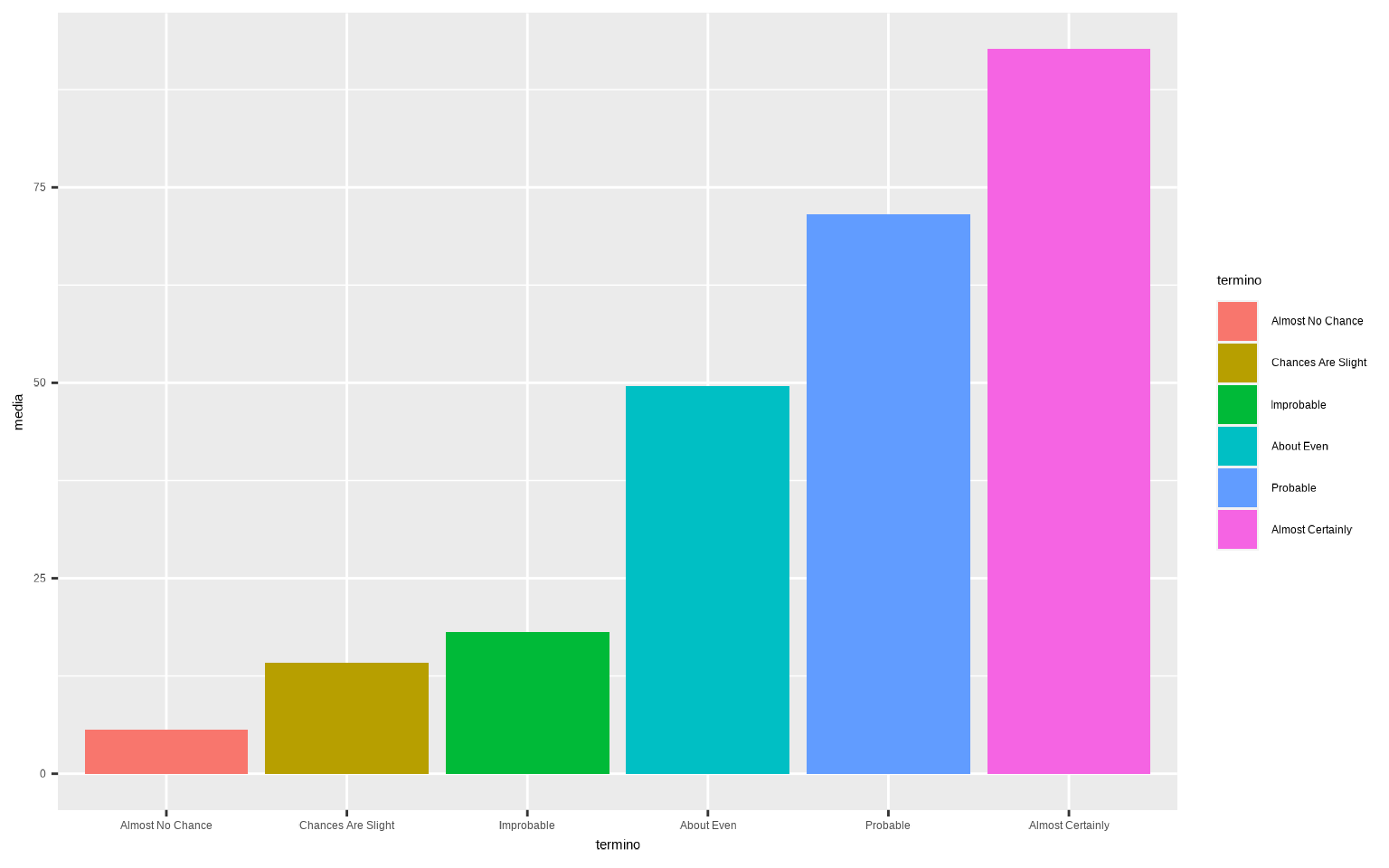
Con scale_fill_brewer() vamos a darle una paleta de colores divergente al relleno, de rojo (poca probabilidad) a azul (mucha probabilidad) con scale_fill_brewer(palette = "RdBu"). Además con scale_x_discrete(labels = ...) vamos a etiquetar correctamente los valores del eje x. Además definiremos un tema para los siguientes gráficos.
library(sysfonts)
library(showtext)
font_add_google(family = "Roboto", name = "Roboto")
showtext_auto()
theme_set(theme_void(base_family = "Roboto"))
theme_update(
axis.text.x =
element_text(color = "black", face = "bold", size = 13),
axis.text.y = element_text(color = "black", size = 9),
axis.line.x = element_line(color = "black", size = 1),
panel.grid.major.y = element_line(color = "grey90", size = 0.7),
plot.background = element_rect(fill = "white", color = "white"),
plot.title = element_text(color = "black", face = "bold",
size = 27),
plot.margin = margin(t = 15, r = 15, l = 15, b = 15))
ggplot(datos_final %>%
group_by(termino) %>%
summarise(media = mean(prob)),
aes(x = termino, y = media, fill = termino)) +
geom_col(alpha = 0.8) +
scale_fill_brewer(palette = "RdBu") +
labs(fill = "Términos",
y = "Probabilidad (%)",
title = "Percepción de la probabilidad")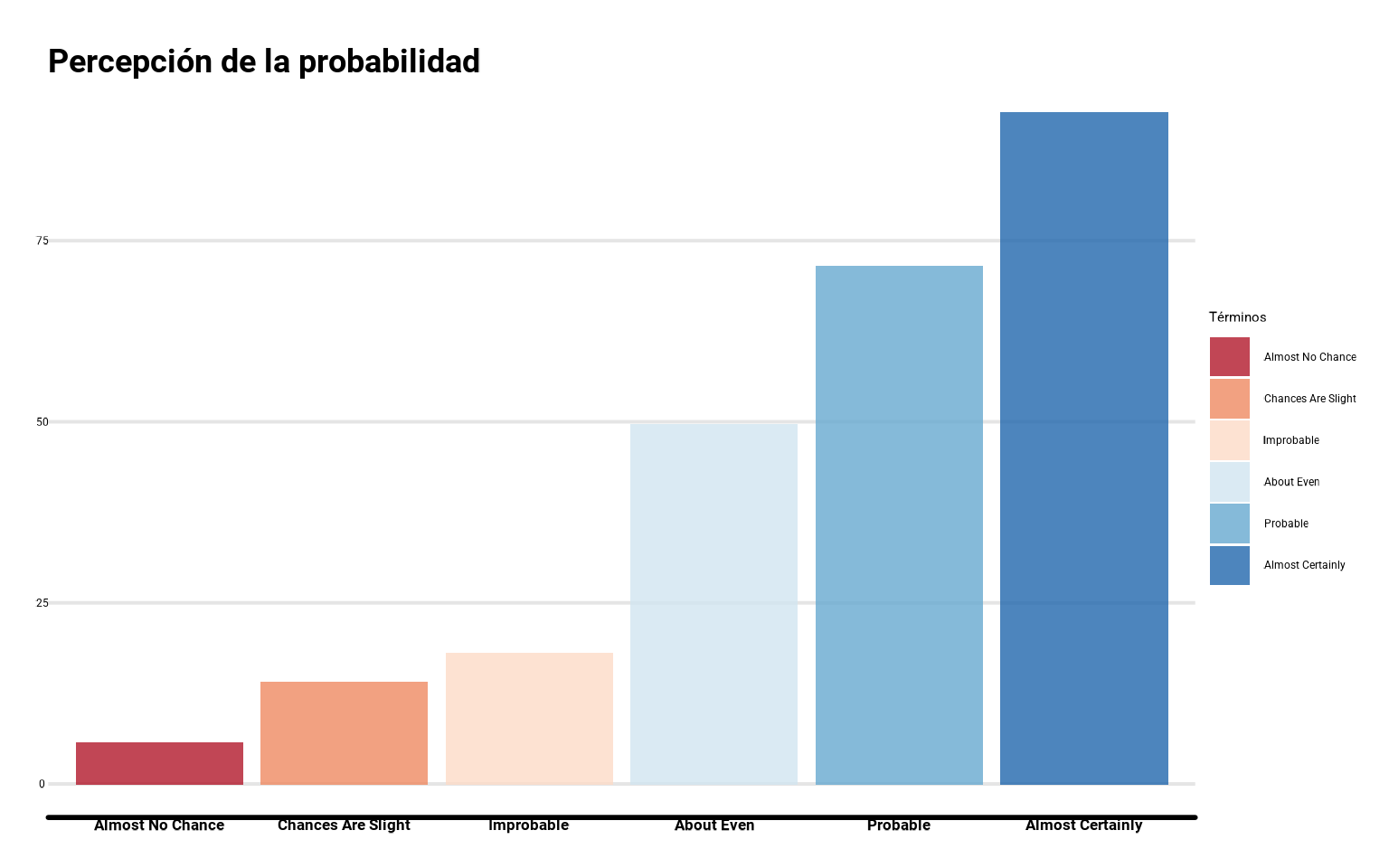
En este caso, para cada variable cualitativa termino, la variable prob es una variable cuantitativa continua, por lo que quizas este tipo de gráficos no tengan mucho sentido ya que resumen demasiado los datos.
¿Cómo podemos visualizar una variable continua?
Una primera opción es usar diagramas de puntos. Para ello primero a preprocesar el conjunto de starwars, filtrando los ausentes en height y species, y recategorizando la variable species en humanos o no humanos.
starwars_altura <-
starwars %>%
drop_na(height, species) %>%
mutate(human = as_factor(species == "Human"))Tras el preprocesado vamos a visualizar con puntos la estatura (variable continua) de cada uno de los dos grupos, haciendo uso de un paquete muy útil llamado ggbeeswarm, un paquete que nos permite con geom_quasirandom() una visualización con puntos de forma que los valores repetidos los reparte aleatoriamente a lo ancho, obteniendo nubes de puntos en lugar de columnas de puntos.
Además le indicaremos con scale_x_discrete() las etiquetas de nuestras categorías (que por defecto sería en inglés, FALSE vs TRUE)
library(ggbeeswarm)
ggplot(starwars_altura,
aes(x = human, y = height,
fill = human, color = human)) +
geom_quasirandom(size = 4.5, width = 0.5, alpha = 0.5) +
scale_x_discrete(labels = c("NO", "SÍ")) +
guides(color = "none", fill = "none") +
labs(x = "¿Son humanos?",
y = "Altura (cm)",
title = "ALTURA DE LOS PERSONAJES DE STARWARS")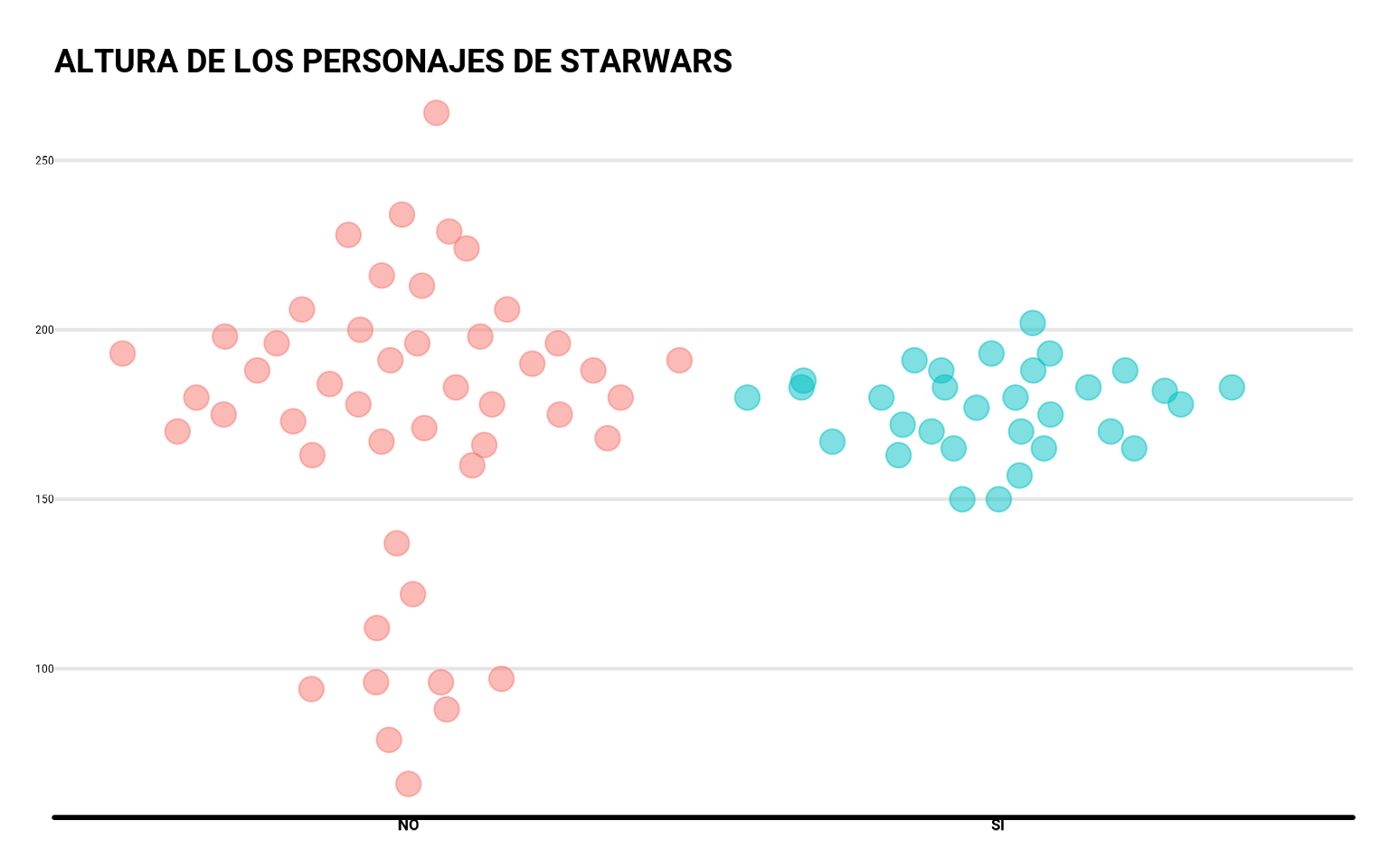
Podemos repetir el gráfico con nuestro conjunto de percepciones de probabilidad.
ggplot(datos_final,
aes(x = termino, y = prob,
fill = termino, color = termino)) +
geom_quasirandom(size = 3.5, width = 0.5,
alpha = 0.7) +
geom_quasirandom(size = 3.5, width = 0.5, shape = 1,
color = "black", stroke = 0.7) +
scale_fill_brewer(palette = "RdBu") +
scale_color_brewer(palette = "RdBu") +
guides(fill = "none") +
labs(color = "Términos", x = "Términos",
y = "Probabilidad (%)",
title = "Percepción de la probabilidad")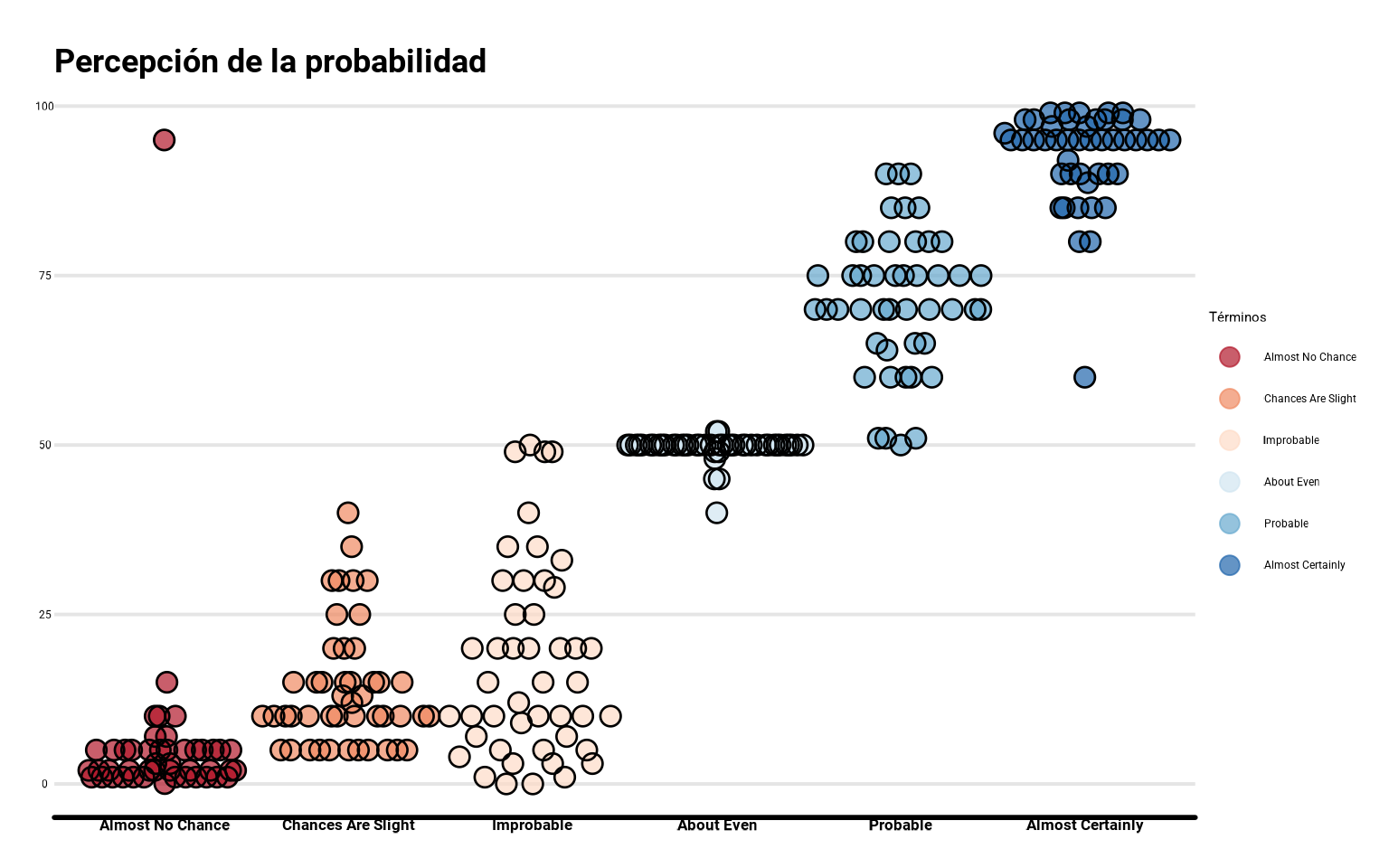
24.2 Cajas y bigotes
Otra opción es con los famosos gráficos de cajas y bigotes con geom_boxplot()
ggplot(datos_final,
aes(x = termino, y = prob, fill = termino)) +
geom_boxplot(alpha = 0.8) +
scale_fill_brewer(palette = "RdBu") +
labs(fill = "Términos",
y = "Probabilidad (%)",
title = "Percepción de la probabilidad")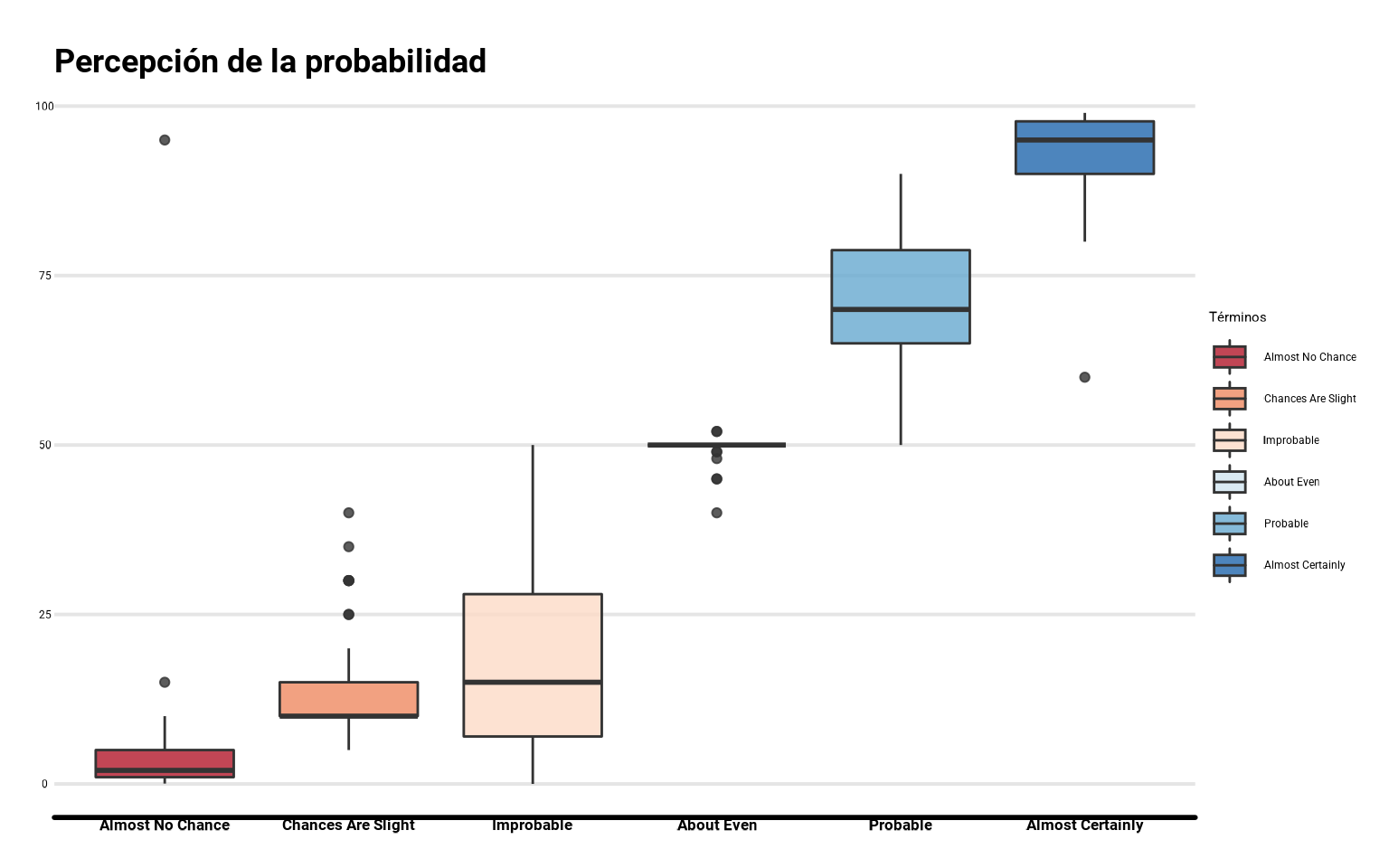
Un diagrama de caja y bigotes o box plot, es un gráfico que resume algunos datos estadísticos en relación a la mediana y medidas de posición (percentiles)
Los lados inferior y superior de la caja representan el primer y tercer cuartil, por lo que la altura de la caja es igual al rango intercuartílico: dentro están el 50% de los datos centrales en torno a la mediana.
La línea gruesa que divide la caja marca la mediana.
Las líneas (bigotes) que salen de las cajas llegan hasta el primer/último dato que no supere 1.5 veces el rango intercuartílico (diferencia entre tercer y primer cuartil). Los puntos alejados representan los datos atípicos o outliers
Es decir, el bigote inferior marca el menor valor por debajo de la caja intercuartílica a distancia menor o igual que 1.5 veces la altura de dicha caja, y el superior marca el mayor valor por encima de la caja intercuartílica a distancia menor o igual que 1.5 veces la altura de dicha caja.
Podemos añadir, además del gráfico resumido, los propios datos con geom_jitter(), que nos añadirá los puntos como una especie de «gotelé aleatorio» (la altura es la de los datos pero la anchura la disemina)
ggplot(datos_final,
aes(x = termino, y = prob,
color = termino, fill = termino)) +
geom_boxplot(alpha = 0.8) +
geom_jitter(alpha = 0.25, size = 1.5) +
scale_fill_brewer(palette = "RdBu") +
scale_color_brewer(palette = "RdBu") +
guides(color = "none", fill = "none")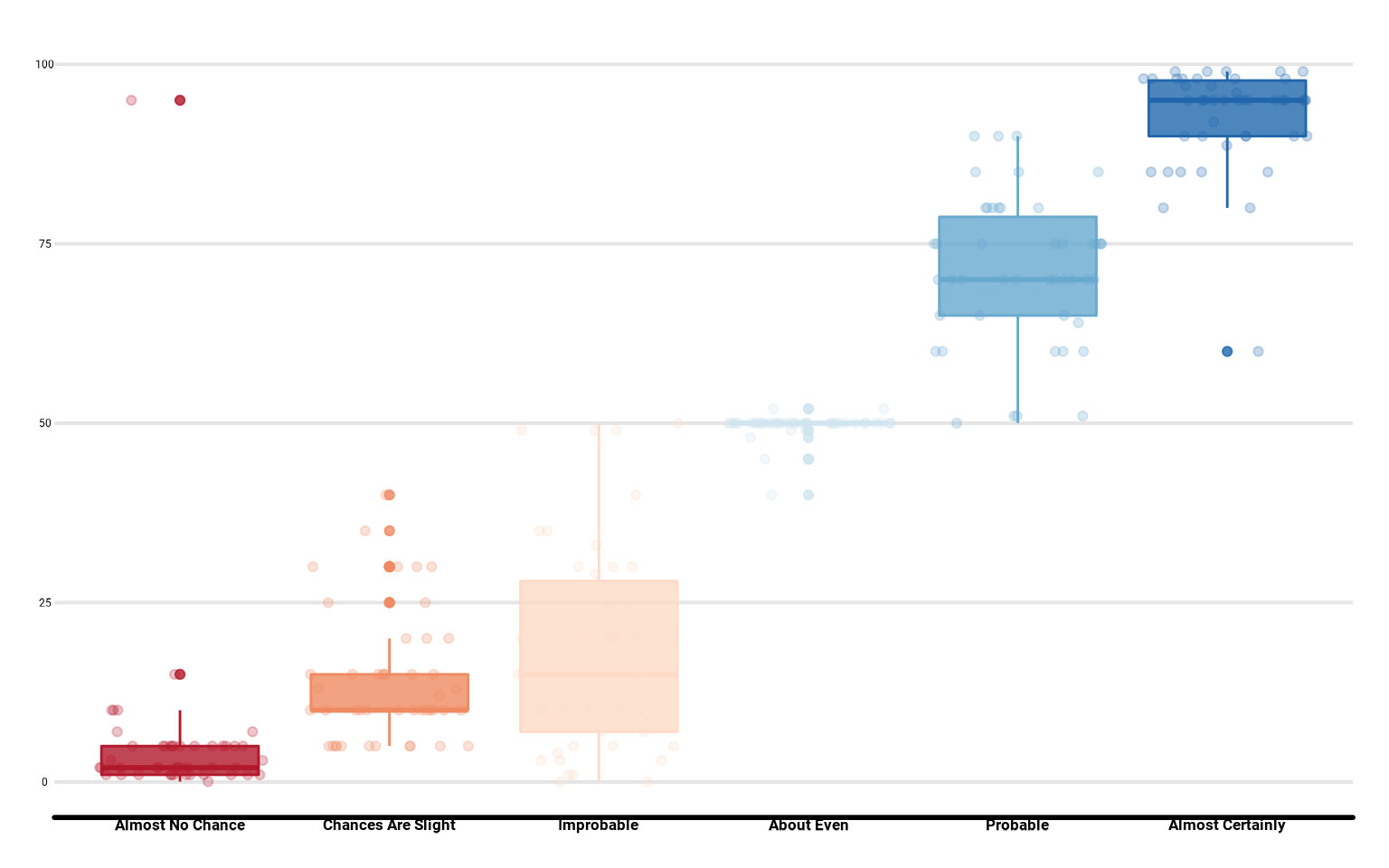
labs(fill = "Términos",
y = "Probabilidad (%)",
title = "Percepción de la probabilidad")## $fill
## [1] "Términos"
##
## $y
## [1] "Probabilidad (%)"
##
## $title
## [1] "Percepción de la probabilidad"
##
## attr(,"class")
## [1] "labels"Con coord_flip() podemos invertir los ejes
ggplot(datos_final,
aes(x = termino, y = prob,
color = termino, fill = termino)) +
geom_boxplot(alpha = 0.8) +
geom_jitter(alpha = 0.25, size = 1.5) +
coord_flip() +
scale_fill_brewer(palette = "RdBu") +
scale_color_brewer(palette = "RdBu") +
guides(color = "none", fill = "none") +
labs(fill = "Términos",
y = "Probabilidad (%)",
title = "Percepción de la probabilidad")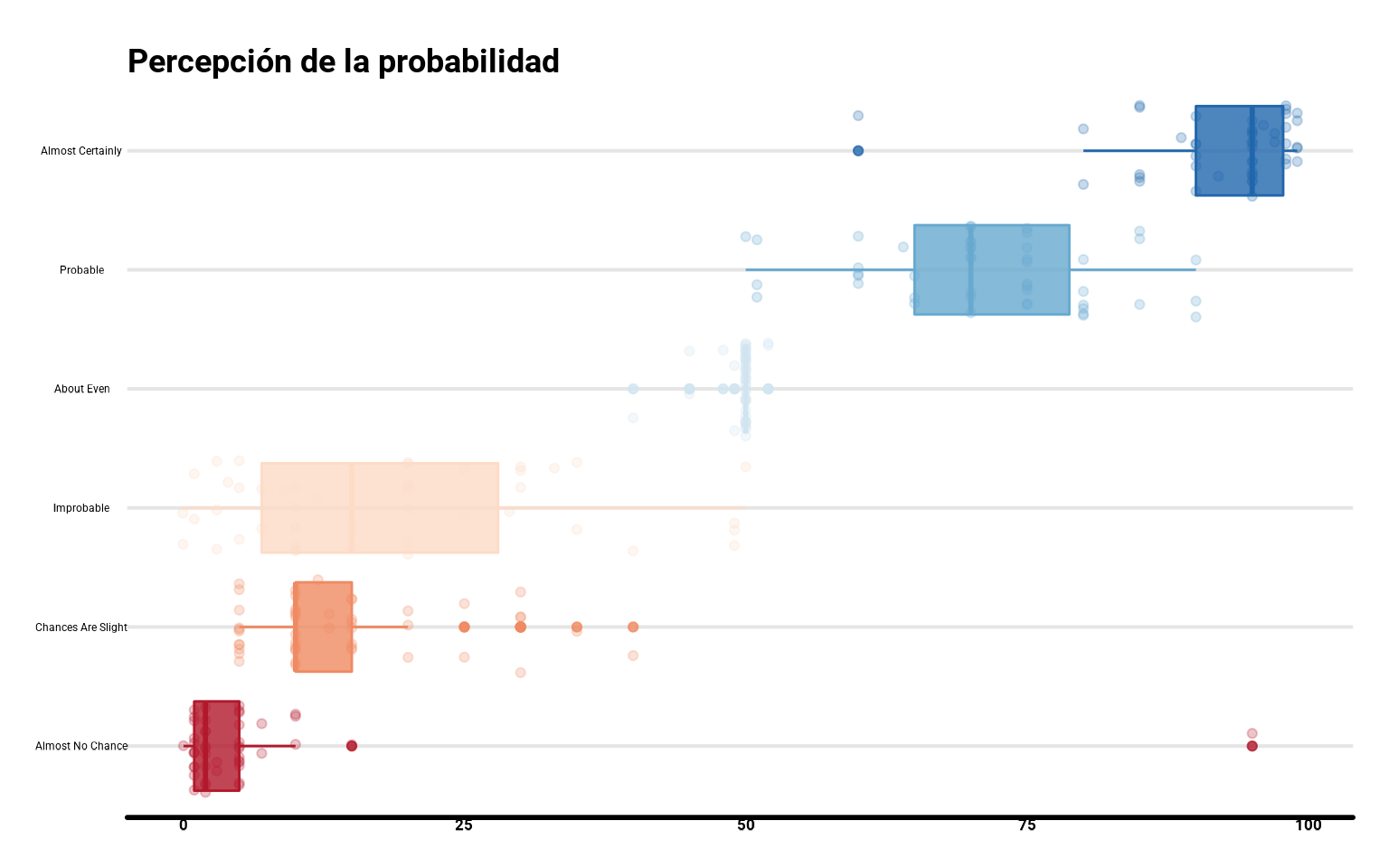
24.3 Histogramas y densidad
Una opción también muy habitual son los gráficos de densidad, que nos representan una versión continua de la distribución empírica de probabilidad.
ggplot(datos_final,
aes(x = prob, color = termino, fill = termino)) +
geom_density(alpha = 0.4) +
scale_fill_brewer(palette = "RdBu") +
scale_color_brewer(palette = "RdBu") +
guides(color = "none") +
labs(fill = "Términos",
y = "Probabilidad (%)",
title = "Percepción de la probabilidad")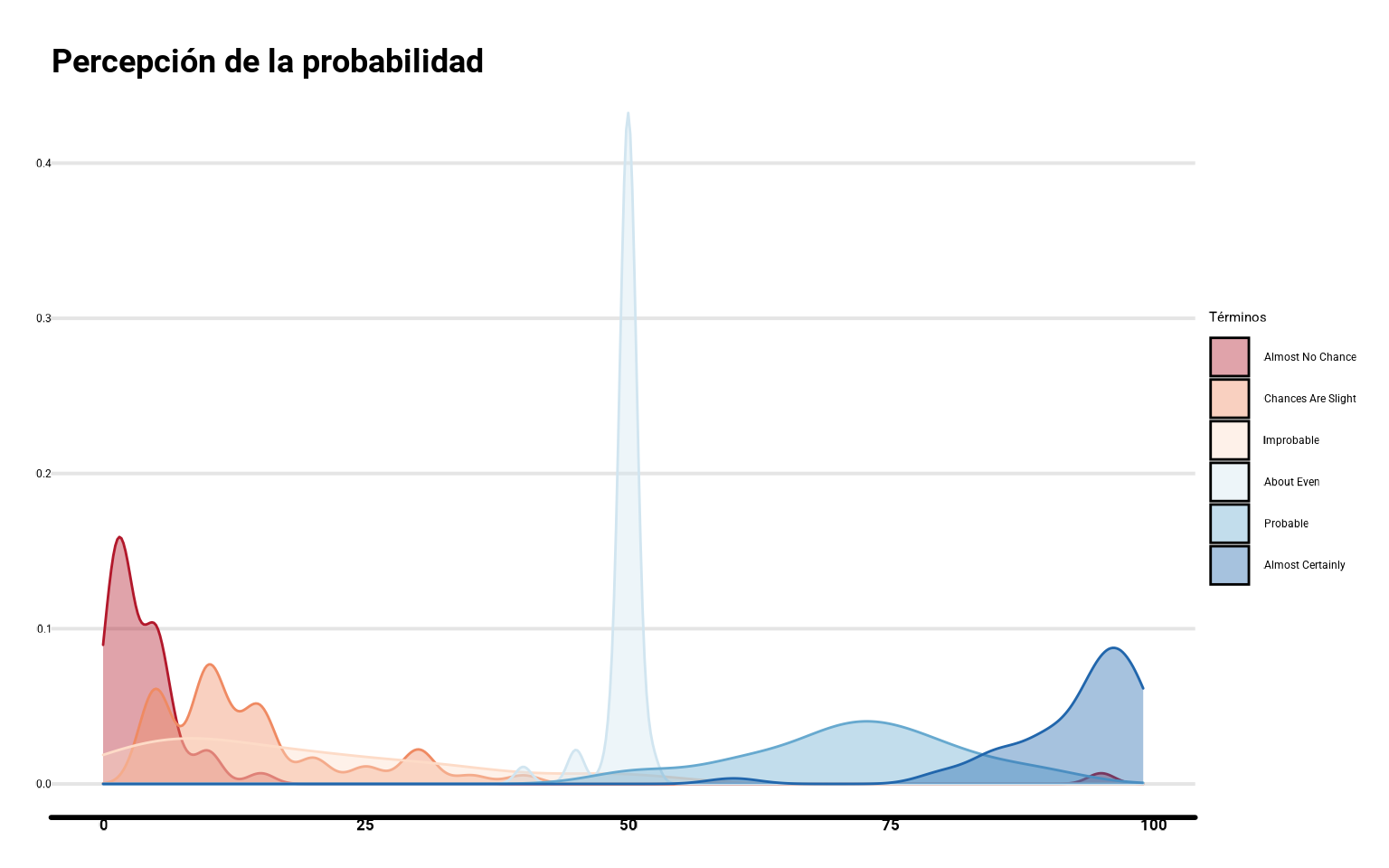
Podemos incluso tomar los datos originales y hacer un panel de las distribuciones de las probabilidades asignadas, componiendo con facet_wrap().
ggplot(datos_pivot %>%
mutate(termino = fct_reorder(termino, prob)),
aes(x = prob, color = termino, fill = termino)) +
geom_density(alpha = 0.4) +
scale_fill_viridis_d() +
scale_color_viridis_d() +
facet_wrap(~ termino, scale = "free_y") +
guides(color = "none", fill = "none") +
labs(fill = "Términos",
y = "Probabilidad (%)",
title = "Percepción de la probabilidad")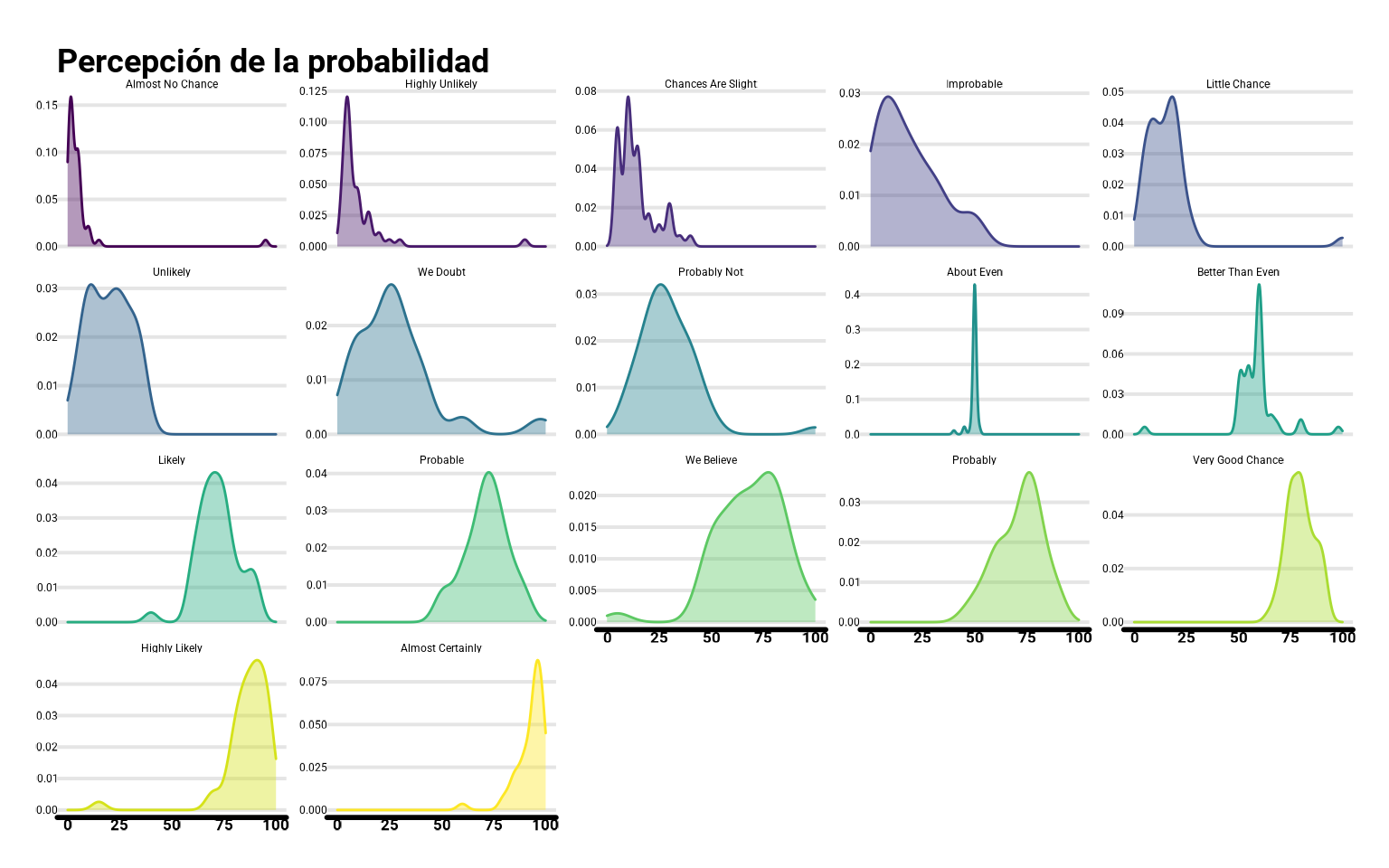
Las funciones de densidad suelen ser aproximadas por lo que se conoce como histograma (que no diagrama de barras). El histograma segmenta en tramos el conjunto de posibles valores y representa la frecuencia de cada uno de esos segmentos como si de un diagrama de barras se tratara (¡pero no lo es! aquí la anchura de la barra no es algo estético sino que representa la amplitud del intervalo). Para pintarlos basta con repetir el proceso anterior, sustituyendo geom_density() por geom_histogram()
ggplot(datos_pivot %>%
mutate(termino = fct_reorder(termino, prob)),
aes(x = prob, color = termino, fill = termino)) +
geom_histogram(alpha = 0.4) +
scale_fill_viridis_d() +
scale_color_viridis_d() +
facet_wrap(~ termino, scale = "free_y") +
guides(color = "none", fill = "none") +
labs(fill = "Términos",
y = "Probabilidad (%)",
title = "Percepción de la probabilidad")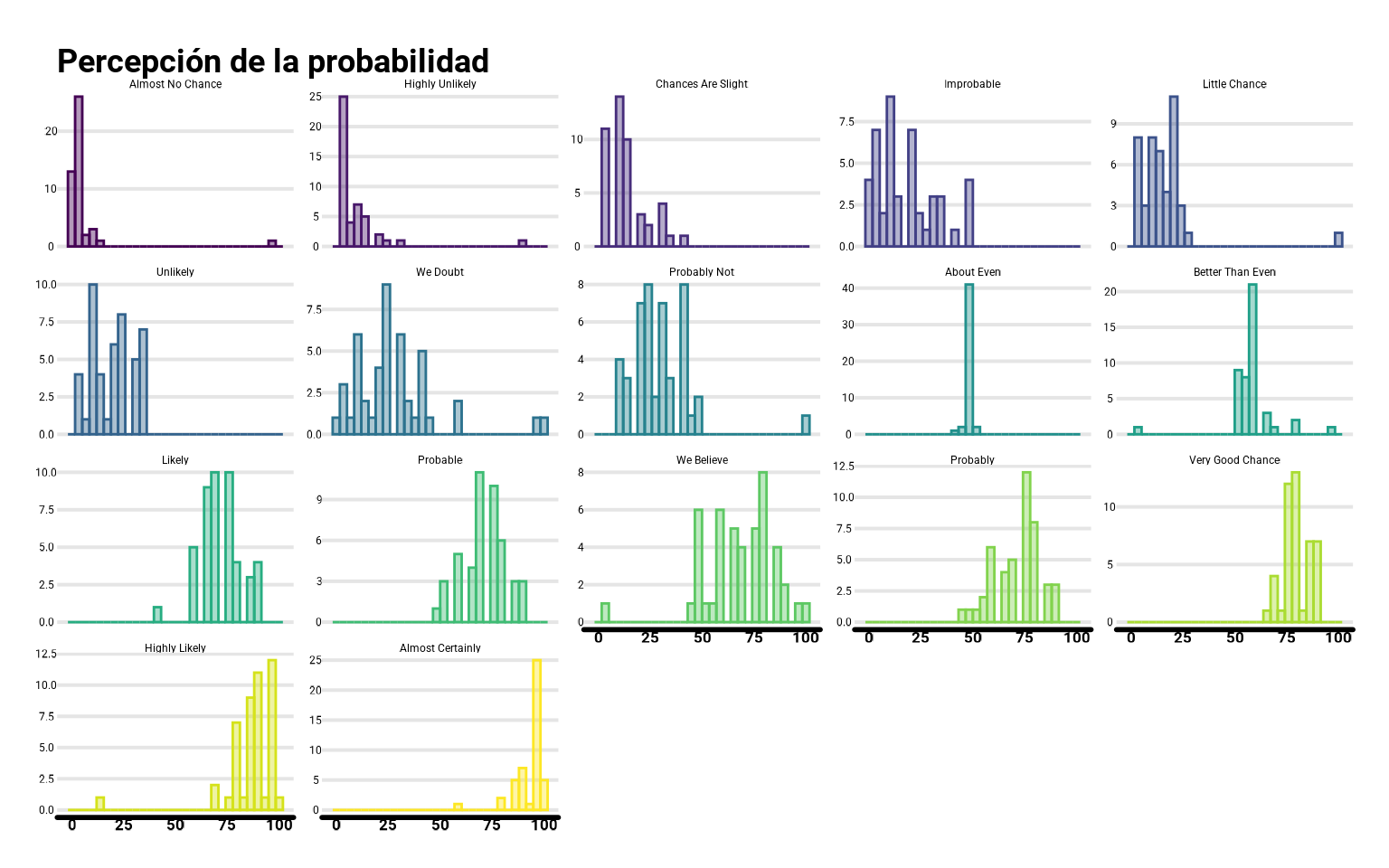
Por defecto nos pinta 30 barras pero podemos indicarle que pinte más o menos, por ejemplo 10 barras con bins = 10.
ggplot(datos_pivot %>%
mutate(termino = fct_reorder(termino, prob)),
aes(x = prob, color = termino, fill = termino)) +
geom_histogram(bins = 10, alpha = 0.4) +
scale_fill_viridis_d() +
scale_color_viridis_d() +
facet_wrap(~ termino, scale = "free_y") +
guides(color = "none", fill = "none") +
labs(fill = "Términos",
y = "Probabilidad (%)",
title = "Percepción de la probabilidad")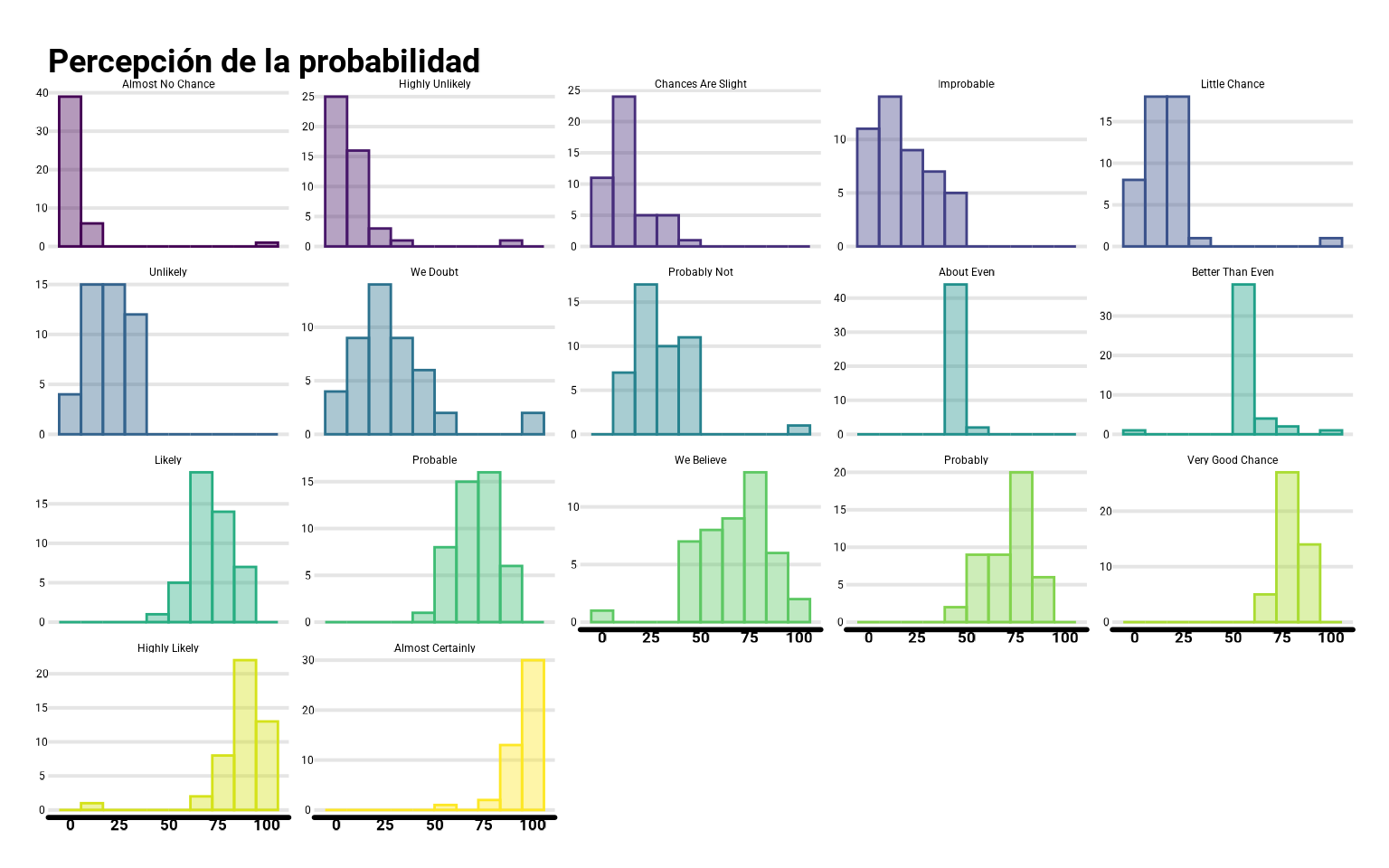
A veces puede ser interesante superponer las densidades, lo cual lo podemos hacer con geom_density_ridges(), del paquete ggridges.
library(ggridges)
ggplot(datos_pivot %>%
mutate(termino = fct_reorder(termino, prob)),
aes(y = termino, x = prob, fill = termino)) +
geom_density_ridges(alpha = 0.4) +
scale_fill_viridis_d() +
scale_color_viridis_d() +
guides(color = "none", fill = "none") +
labs(fill = "Términos",
y = "Probabilidad (%)",
title = "Percepción de la probabilidad")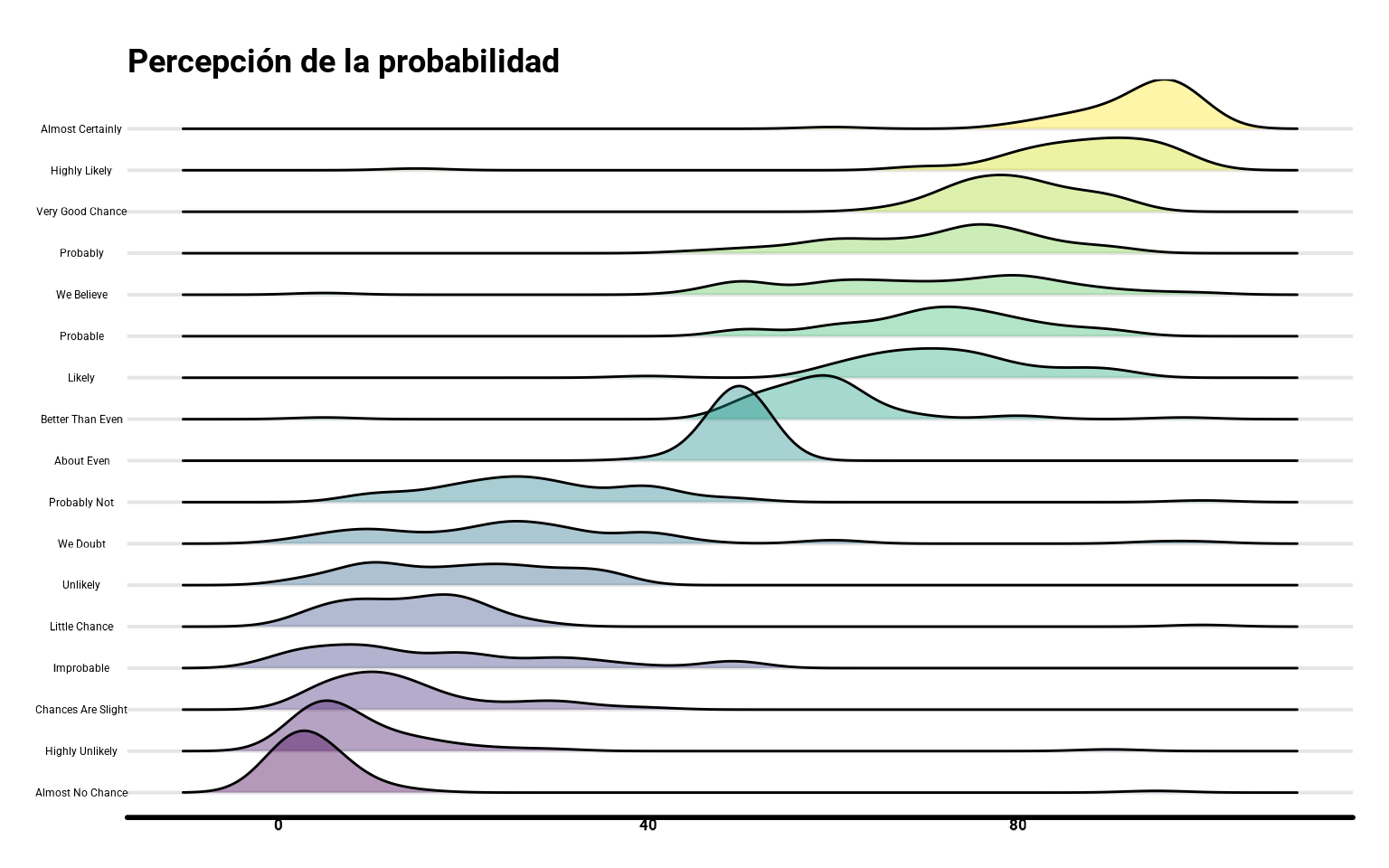
Como hemos comentado, los gráficos de densidad son una versión continua, asintótica si queremos, de un histograma (algo así como la integral lo es a la suma infinita), asumiendo que los intervalos se pudieran ir haciendo tan pequeños como queramos, generado una curva continua. Las densidades mejoran la robustez al histograma que puede variar mucho en función de los tramos de agregación elegidos.
24.4 Gráficos de violín
Una alternativa a los gráficos de cajas y bigotes, con el objetivo de poder ver la distribución real que dicho gráfico nos simplifica, son los gráficos de violín, que podemos realizar con geom_violin().
ggplot(datos_final,
aes(y = termino, x = prob,
fill = termino)) +
geom_violin(size = 1) +
scale_fill_brewer(palette = "RdBu") +
guides(fill = "none") +
labs(y = "Probabilidad (%)",
title = "Percepción de la probabilidad")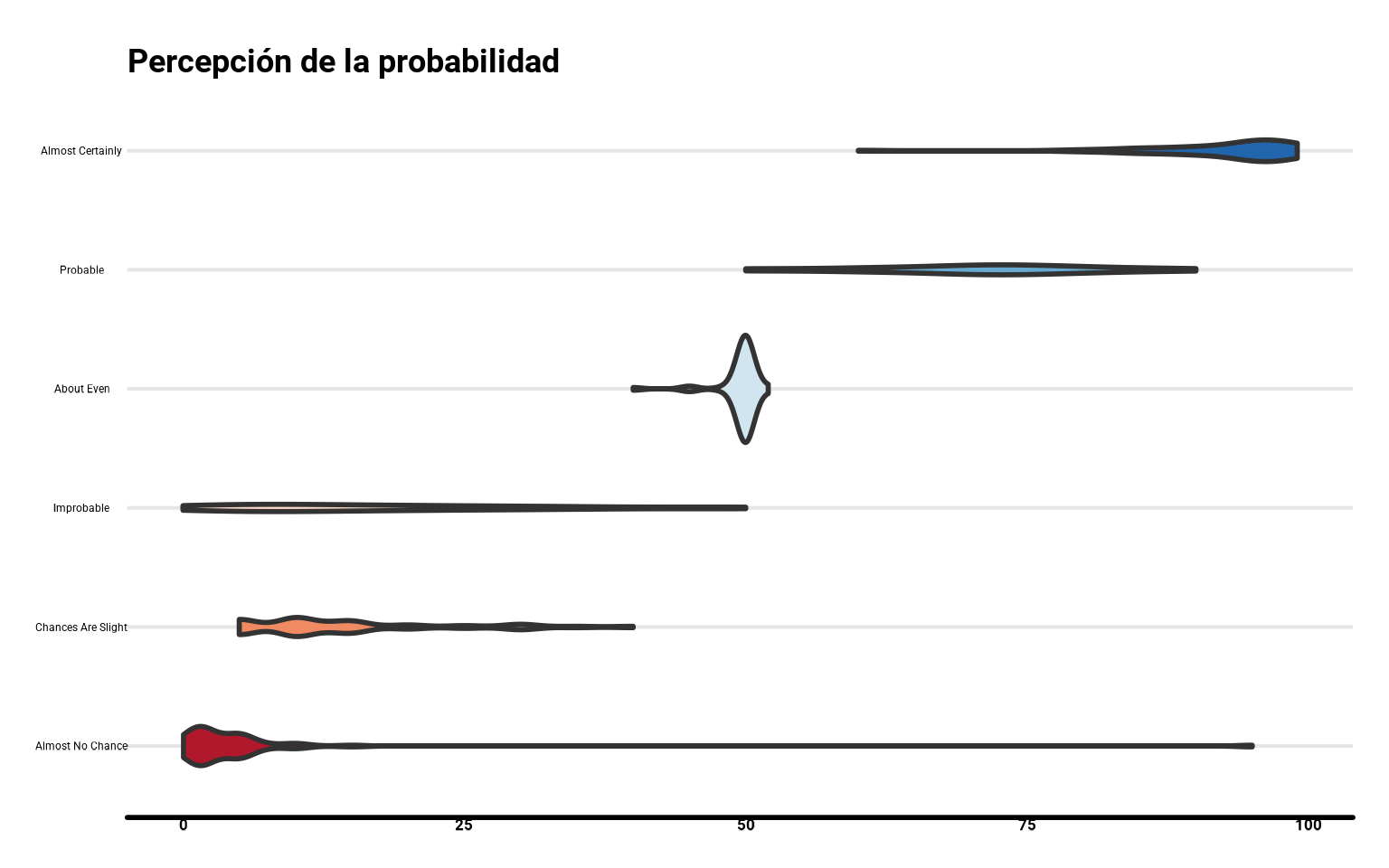
Podemos añadir la línea de contorno del mismo color, y para distinguirlo del relleno, vamos a clarear el color con lighten, del paquete colorspace (con after_scale, para que el mapeado lo realiza tras evaluar y escalar los datos).
library(colorspace)
ggplot(datos_final,
aes(y = termino, x = prob)) +
geom_violin(aes(fill = termino, color = termino,
fill = after_scale(lighten(fill, .4))),
size = 1) +
scale_fill_brewer(palette = "RdBu") +
scale_color_brewer(palette = "RdBu") +
guides(color = "none", fill = "none") +
labs(y = "Probabilidad (%)",
title = "Percepción de la probabilidad")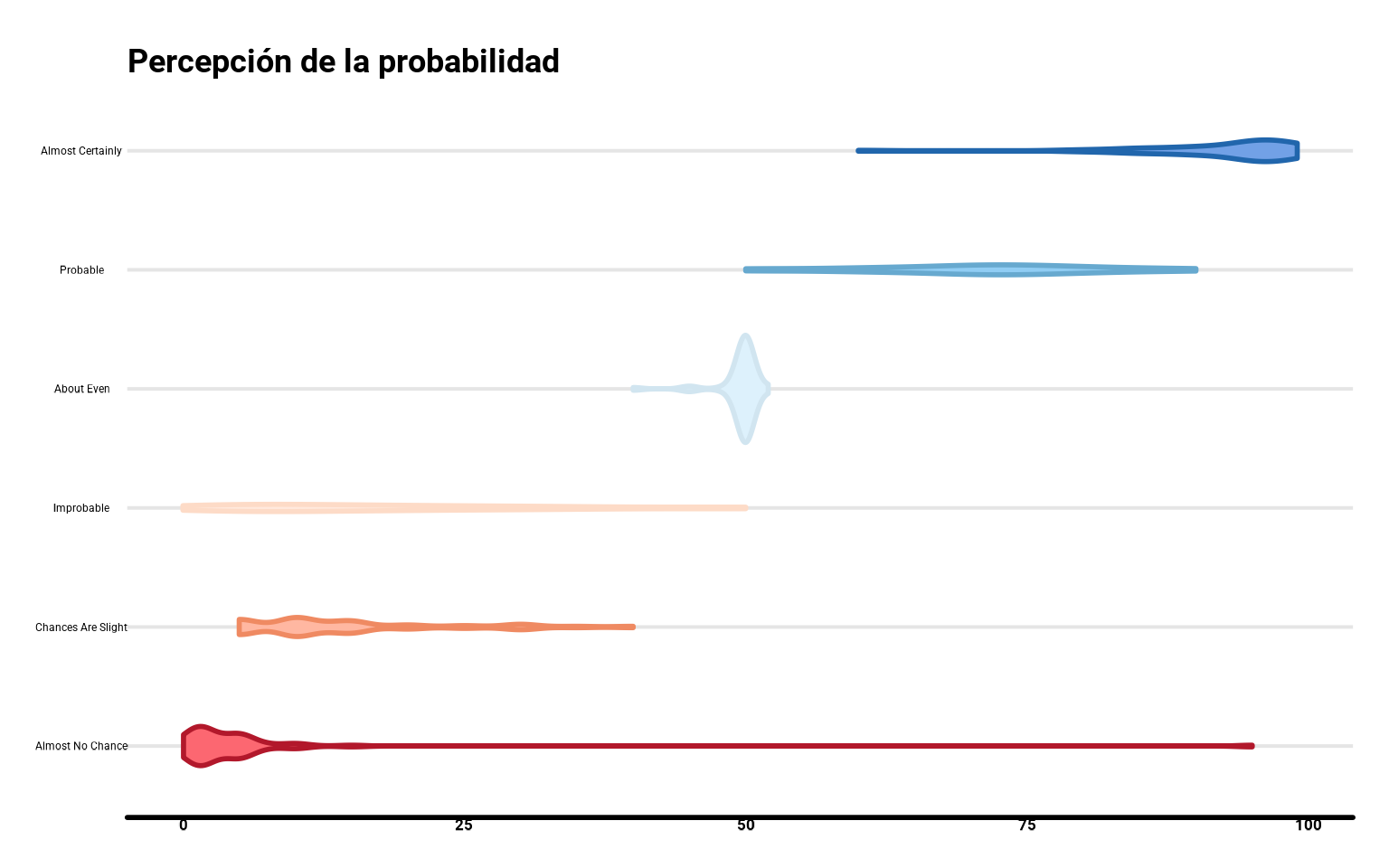
Dentro de geom_violin(), con el parámetro bw podemos ajustar el ancho de banda: a mayor valor, más suaves serán las figuras.
ggplot(datos_final,
aes(y = termino, x = prob)) +
geom_violin(aes(fill = termino, color = termino,
fill = after_scale(lighten(fill, .4))),
size = 1, bw = 1.5) +
scale_fill_brewer(palette = "RdBu") +
scale_color_brewer(palette = "RdBu") +
guides(color = "none", fill = "none") +
labs(y = "Probabilidad (%)",
title = "Percepción de la probabilidad")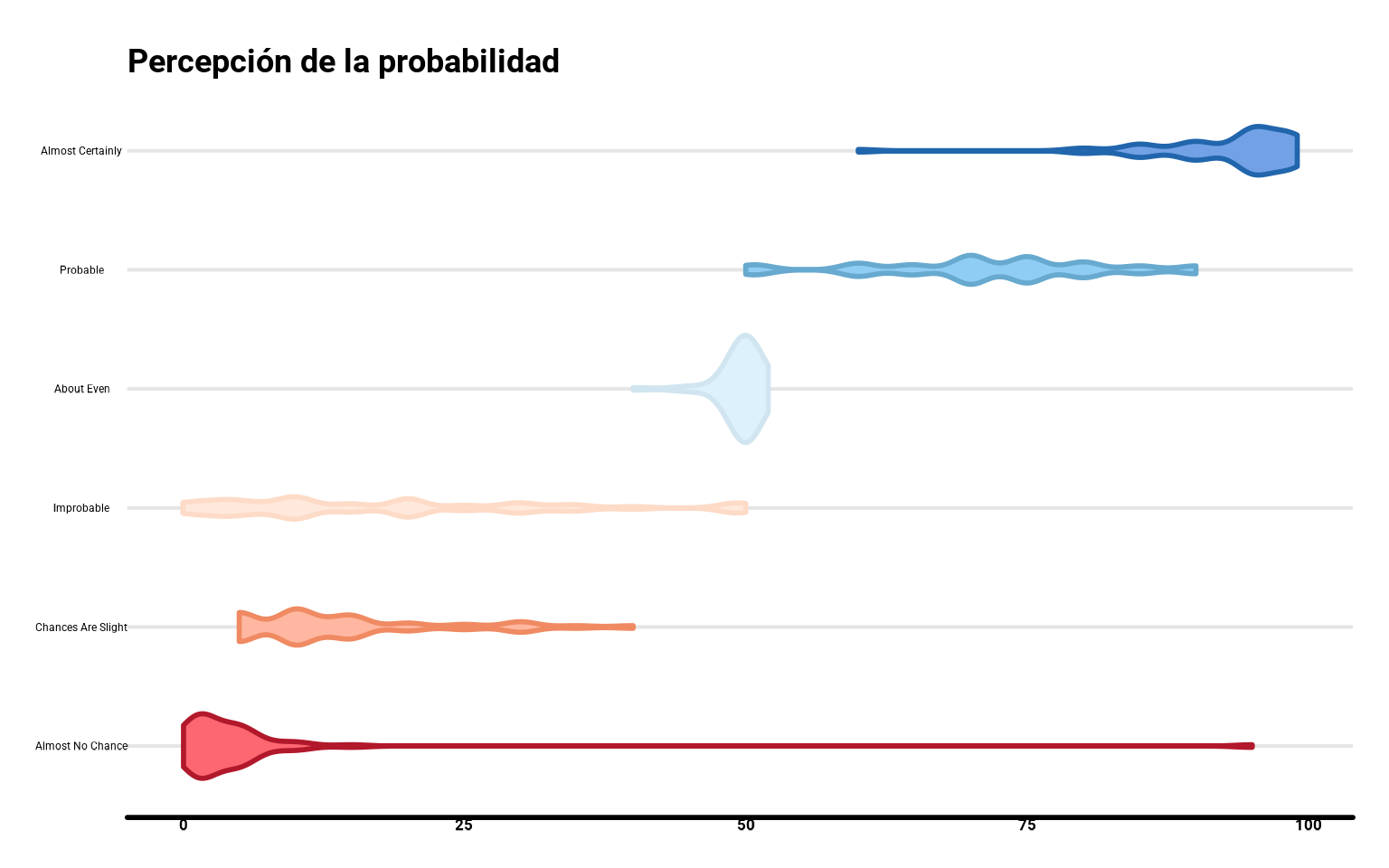
Como todos los gráficos podemos invertir la dirección, pasando de horizontal a vertical, con coord_flip().
ggplot(datos_final,
aes(y = termino, x = prob)) +
geom_violin(aes(fill = termino, color = termino,
fill = after_scale(lighten(fill, .4))),
size = 1, bw = 1.5) +
scale_fill_brewer(palette = "RdBu") +
scale_color_brewer(palette = "RdBu") +
coord_flip() +
guides(color = "none", fill = "none") +
labs(y = "Probabilidad (%)",
title = "Percepción de la probabilidad")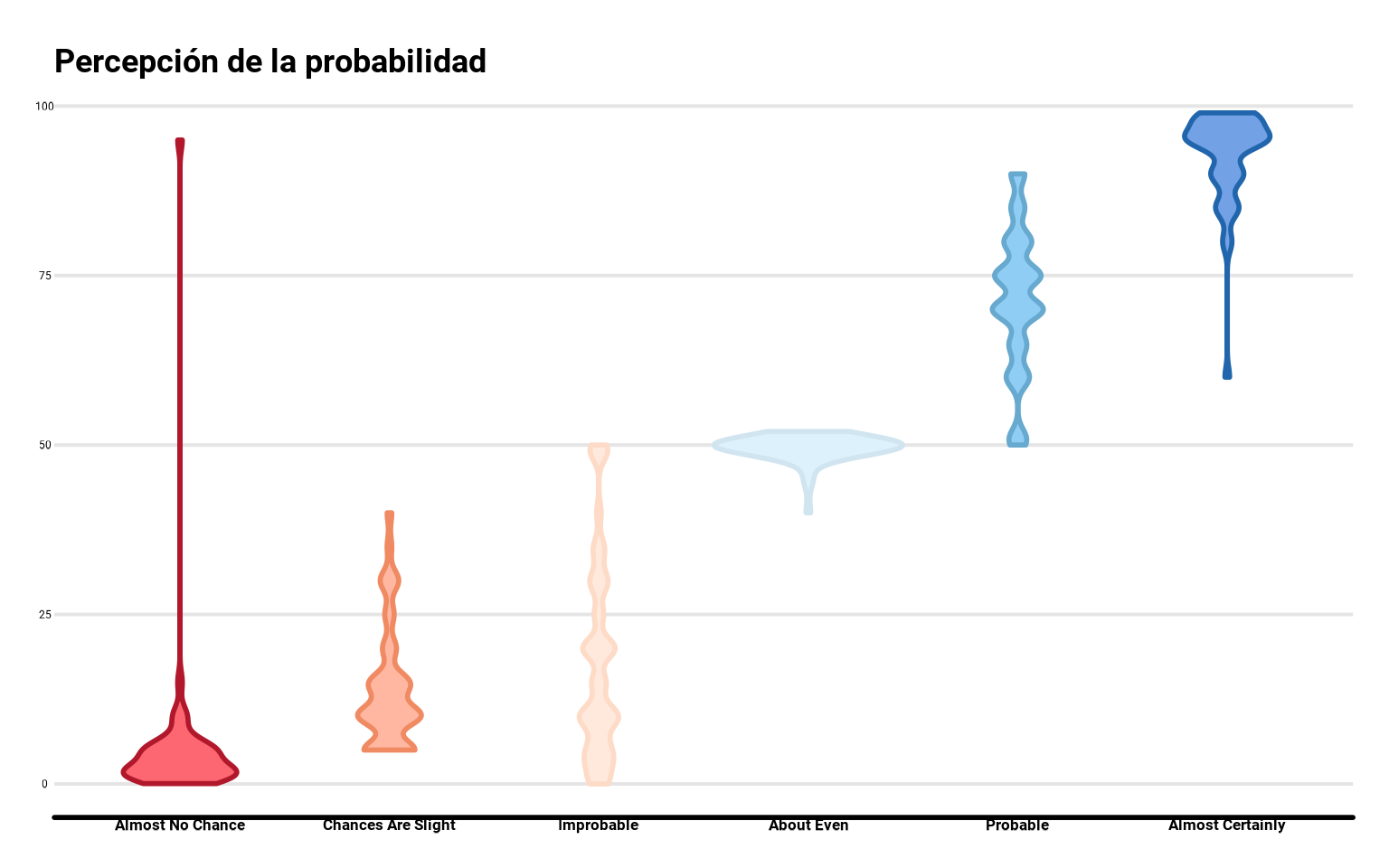
24.5 Half-eye plots
El paquete ggdist también contiene numerosas herramientas para visualizar distribuciones continuas e intervalos, como la función stat_halfeye() que nos permite visualizar los conocidos como half-eye plots (con adjust podemos ajustar el ancho de banda con el que estima la densidad). En este caso además nos pinta la mediana como un punto.
library(ggdist)
ggplot(datos_final,
aes(y = termino, x = prob)) +
stat_halfeye(aes(fill = termino,
fill = after_scale(lighten(fill, .5))),
.width = 0.5, adjust = 0.7, point_size = 2) +
scale_fill_brewer(palette = "RdBu") +
scale_color_brewer(palette = "RdBu") +
coord_flip() +
guides(color = "none", fill = "none") +
labs(y = "Probabilidad (%)",
title = "Percepción de la probabilidad")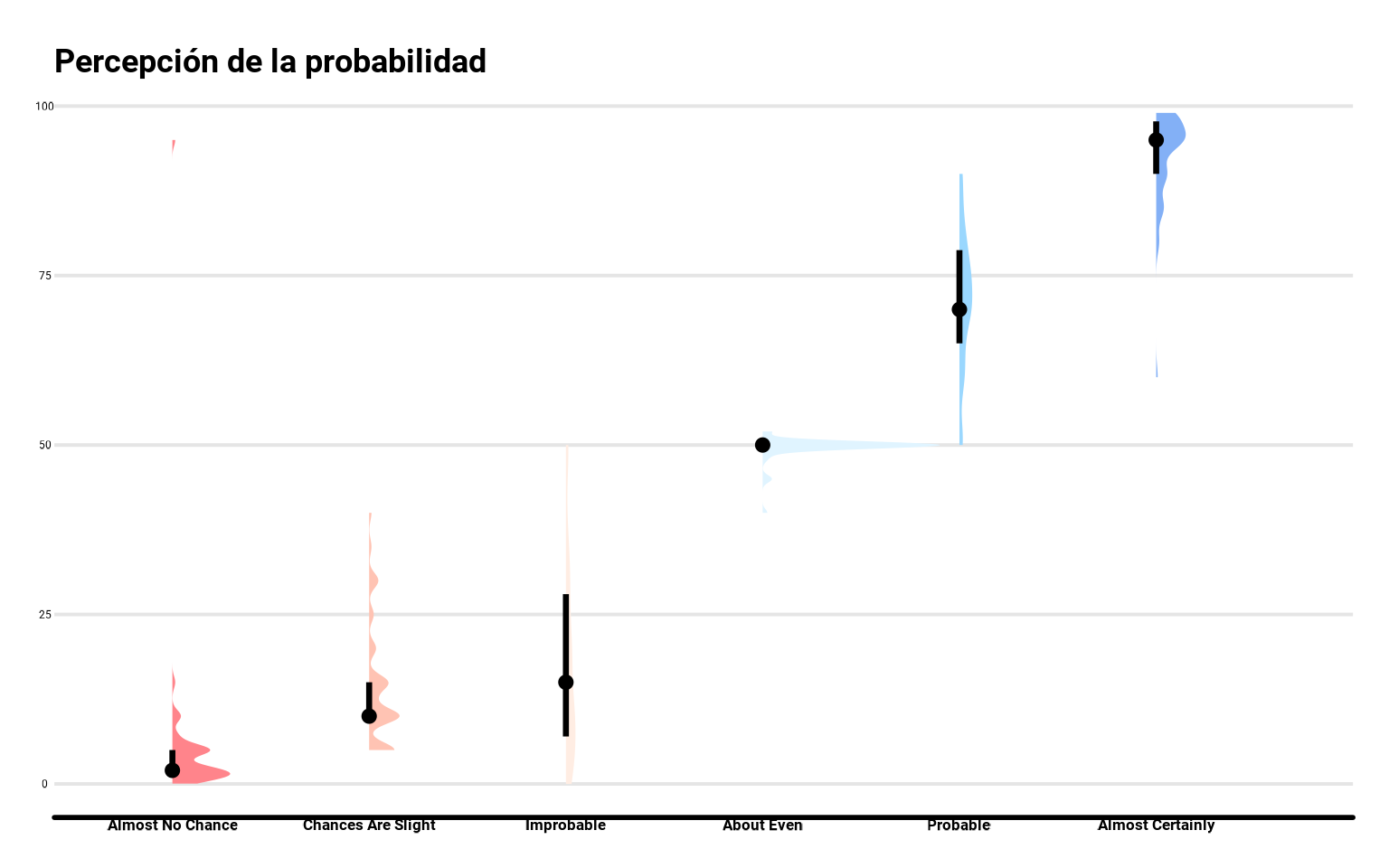
24.6 📝 Ejercicios
(haz click en las flechas para ver soluciones)
En la carpeta DATOS, en el fichero coches.csv, dispones de una tabla que contiene información de distintos tipos de vehículos. La información que contiene es:
-
name: nombre del vehículo -
sports_car, suv, wagon, minivan, pickup, all_wheel, rear_wheel: variables lógicas, nos dicen si son de ese tipo o no. -
msrp: precio de fábrica -
dealer_cost: precio de coste -
eng_size: tamaño del motor -
ncyl: número de cilindros -
city_mpg, hwy_mpg: consumo en distintos entornos -
weight, wheel_base, length, width: distintas medidas de dimensión del vehículo
📝Ejercicio 1: genera una columna de tipo factor que aglutine las columnas binarias
sports_car, suv, wagon, minivan, pickup en una sola que contenga el tipo (por ejemplo, si suv es TRUE, esa columna contendrá "suv")
- Solución:
library(tidyverse)
coches <- read_csv("./DATOS/coches.csv")
coches <-
coches %>%
mutate(tipo =
case_when(sports_car ~ "sports_car",
suv ~ "suv",
wagon ~ "wagon",
minivan ~ "minivan",
pickup ~ "pickup",
all_wheel ~ "all_wheel",
rear_wheel ~ "rear_wheel",
TRUE ~ "otros"),
tipo = as_factor(tipo)) %>%
select(-c(sports_car, suv, wagon, minivan, pickup))
fct_count(coches$tipo)## # A tibble: 8 × 2
## f n
## <fct> <int>
## 1 otros 166
## 2 all_wheel 25
## 3 rear_wheel 54
## 4 sports_car 49
## 5 suv 60
## 6 wagon 30
## 7 minivan 20
## 8 pickup 24
📝Ejercicio 2: para ver si hay diferencia de consumo, ¿podrías calcular la media y desviación de
city_mpg y hwy_mpg? Haz un diagrama que permita hacernos una idea de cómo se distribuye el consumo.
- Solución:
coches %>%
summarise_at(vars(c("city_mpg", "hwy_mpg")),mean, na.rm = TRUE)## # A tibble: 1 × 2
## city_mpg hwy_mpg
## <dbl> <dbl>
## 1 20.1 26.9
coches %>%
summarise_at(vars(c("city_mpg", "hwy_mpg")),
sd, na.rm = TRUE)## # A tibble: 1 × 2
## city_mpg hwy_mpg
## <dbl> <dbl>
## 1 5.21 5.70
# densidades
ggplot(coches %>%
pivot_longer(cols = c("city_mpg", "hwy_mpg"),
names_to = "consumo",
values_to = "values") %>%
drop_na(values),
aes(x = values, fill = consumo)) +
geom_density(alpha = 0.5) +
scale_fill_discrete(labels = c("Ciudad", "Autopista"))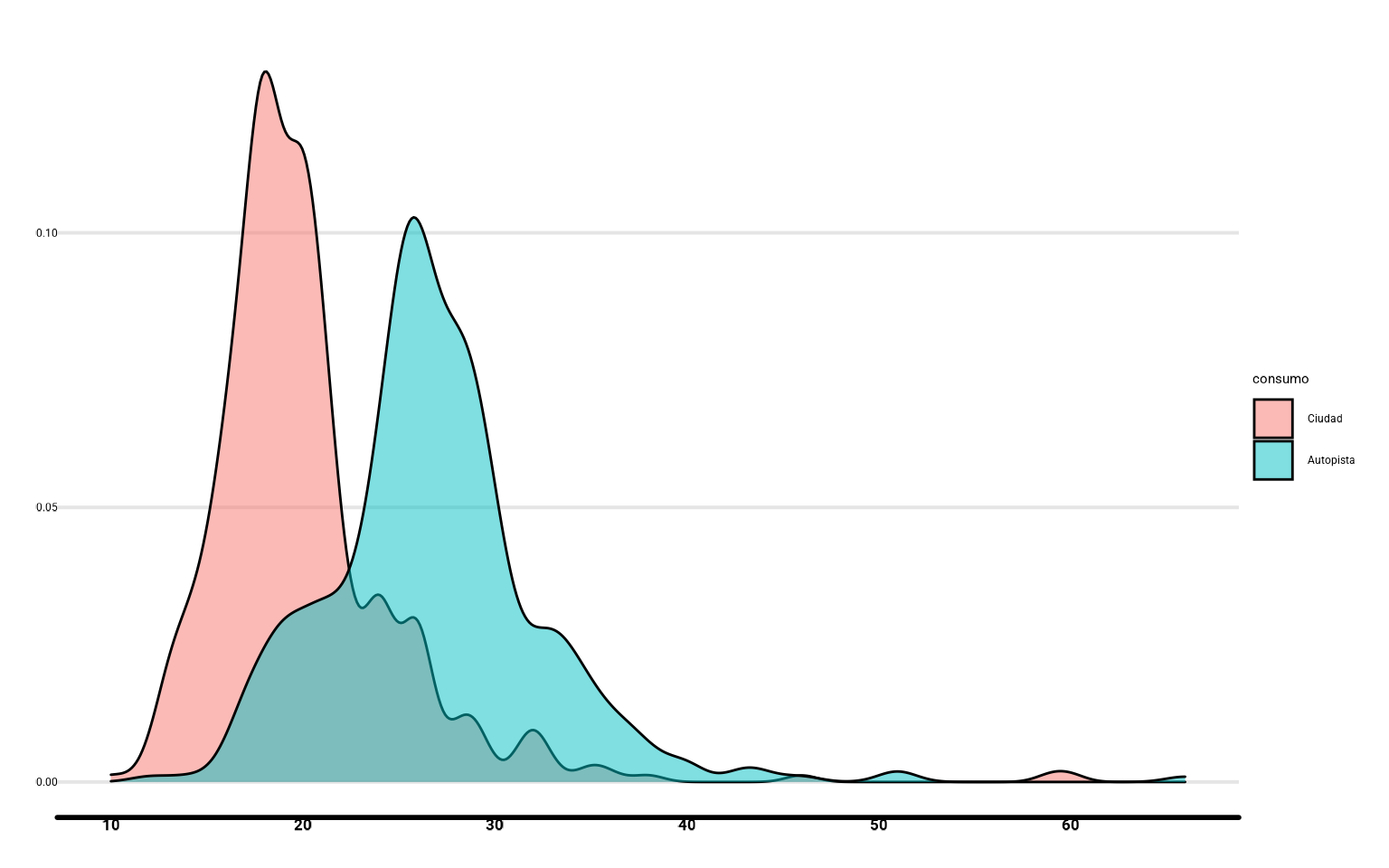
labs(y = "densidad", x = "consumo (mpg)",
fill = "Consumo")## $y
## [1] "densidad"
##
## $x
## [1] "consumo (mpg)"
##
## $fill
## [1] "Consumo"
##
## attr(,"class")
## [1] "labels"
📝Ejercicio 3: para ver si hay diferencia de consumo por tipo de coche, calcula la media de
city_mpg y hwy_mpg para los distintos tipos de coche.
- Solución:
coches %>%
group_by(tipo) %>%
summarise_at(vars(c("city_mpg", "hwy_mpg")),
c(mean = mean, sd = sd), na.rm = TRUE)## # A tibble: 8 × 5
## tipo city_mpg_mean hwy_mpg_mean city_mpg_sd hwy_mpg_sd
## <fct> <dbl> <dbl> <dbl> <dbl>
## 1 otros 23.6 31.3 6.19 5.49
## 2 all_wheel 18.6 25.8 1.71 1.83
## 3 rear_wheel 18.0 25.5 1.48 2.35
## 4 sports_car 18.6 25.7 2.53 2.72
## 5 suv 16.2 20.6 2.73 3.22
## 6 wagon 21.0 27.8 4.22 4.45
## 7 minivan 17.9 24.4 1.45 2.46
## 8 pickup 16.7 21.2 3.24 3.82
ggplot(coches %>% filter(tipo != "otros") %>%
pivot_longer(cols = c("city_mpg", "hwy_mpg"),
names_to = "consumo",
values_to = "values") %>%
drop_na(values), aes(x = values, fill = consumo)) + geom_density(alpha = 0.5) + facet_wrap( ~ tipo)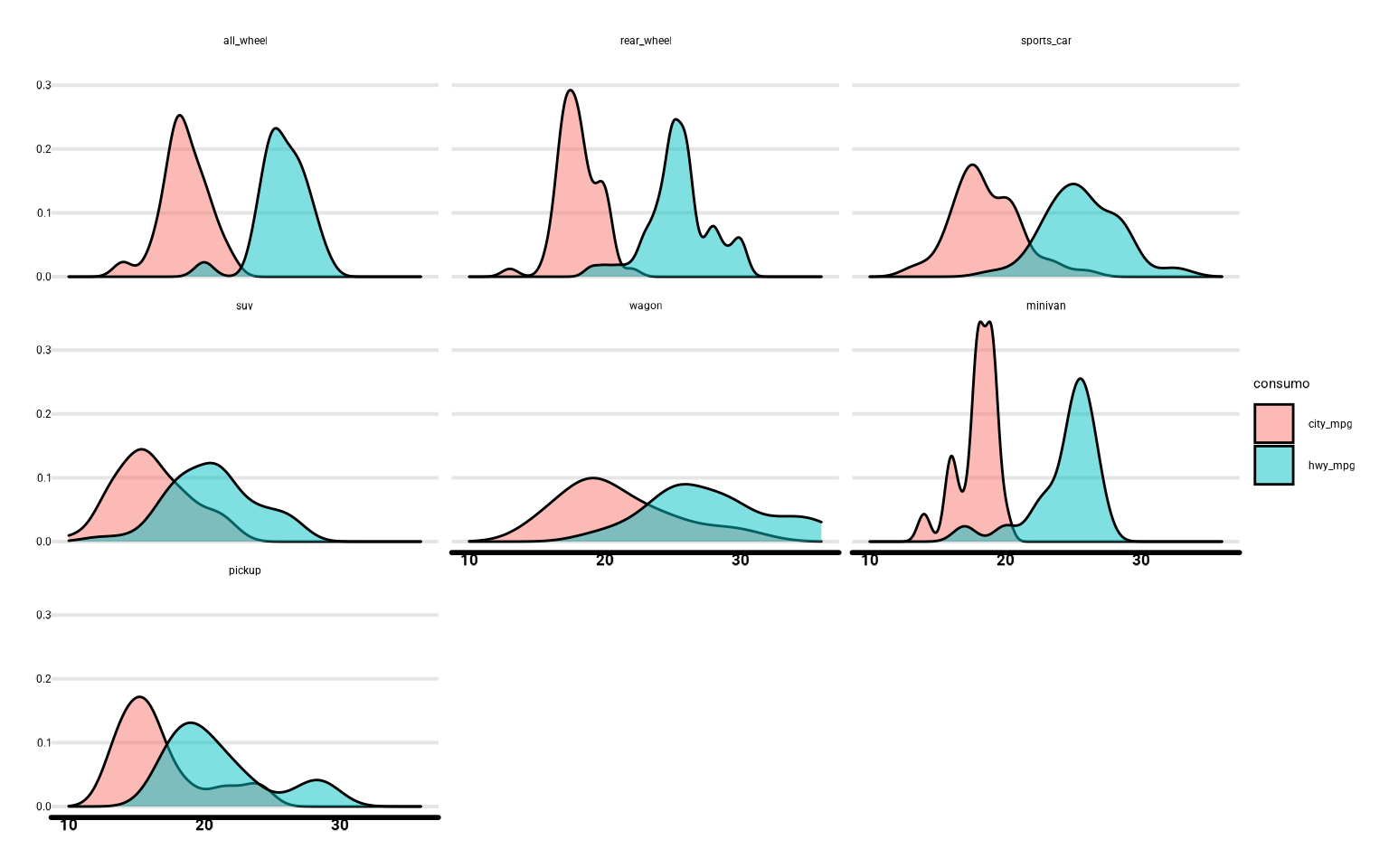
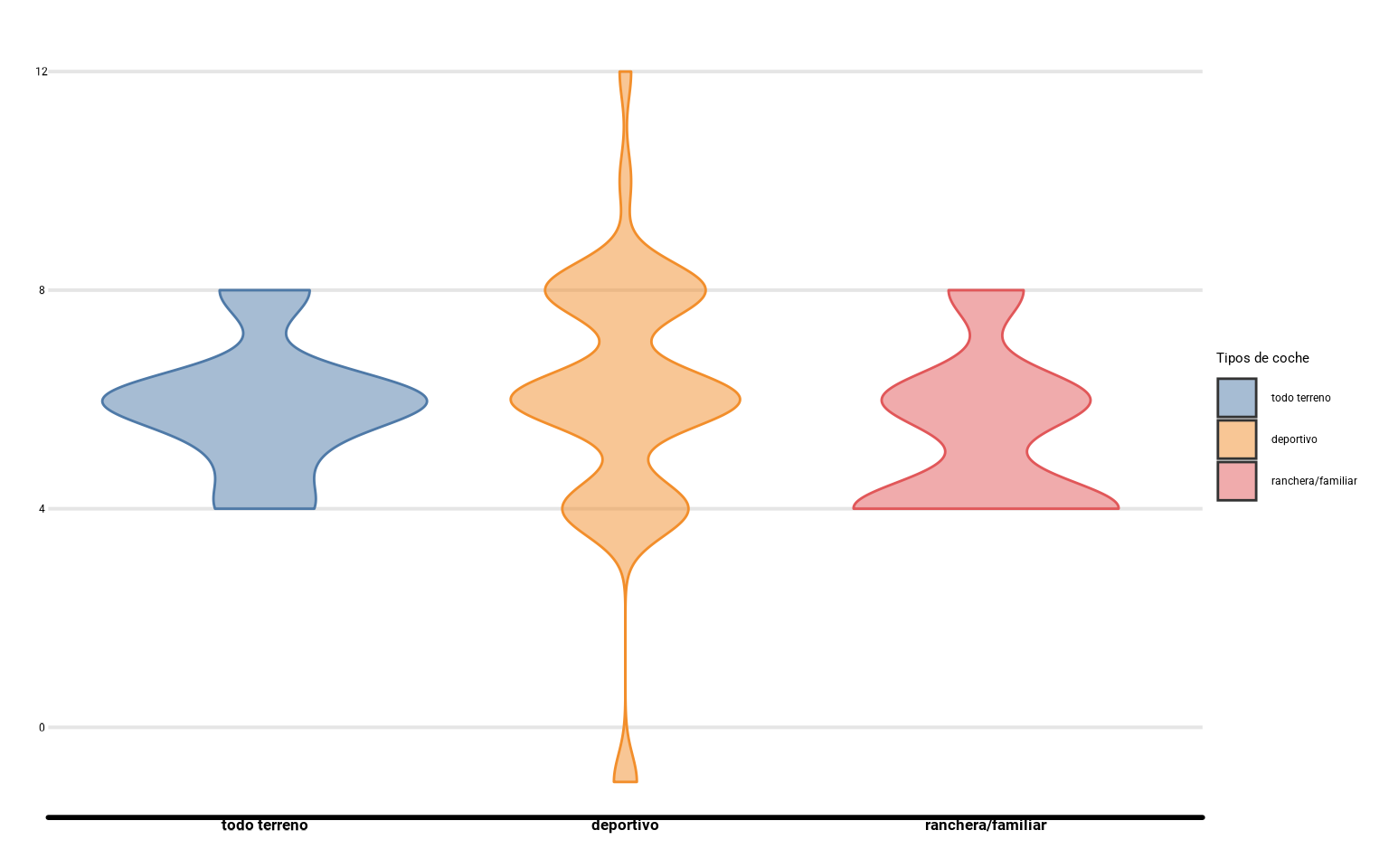
📝Ejercicio 4: a la vista de los resultados previos, seleccionar los 3 tipos de mayor consumo, filtra la tabla y representa la variable
cyl con un gráfico de violín
- Solución:
coches_filtro <-
coches %>%
filter(tipo %in%
c("wagon", "all_wheel", "sports_car"))
library(ggthemes)
ggplot(coches_filtro,
aes(x = tipo, y = ncyl,
fill = tipo, color = tipo)) +
geom_violin(alpha = 0.5, bw = 0.5) +
scale_fill_tableau(labels = c("todo terreno",
"deportivo",
"ranchera/familiar")) +
scale_color_tableau() +
guides(color = "none") +
scale_x_discrete(labels = c("todo terreno", "deportivo",
"ranchera/familiar")) +
labs(fill = "Tipos de coche",
x = "Tipos de coche", y = "Cilindrada")